练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB=AC，∠A=36°，直线MN垂直平分AC交AB于M，

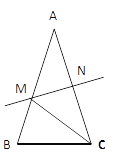
    （1）求∠BCM的度数；（2）若AB=5，BC=3，求△BCM的周长.

    【答案】（1）36°；（2）8.

    【解析】

    （1）由AB＝AC，∠A＝36°，可求得∠ACB的度数，又由直线MN垂直平分AC交AB于M，根据线段垂直平分线的性质，可求得AM＝CM，即可求得∠ACM的度数，继而求得∠BCM的度数；

    （2）由AM＝CM，可得△BCM的周长＝BC＋AB．

    解：（1）∵AB＝AC，∠A＝36°，

    ∴∠B＝∠ACB＝72°，

    ∵直线MN垂直平分AC交AB于M，

    ∴AM＝CM，

    ∴∠ACM＝∠A＝36°，

    ∴∠BCM＝∠ACB∠ACM＝36°；

    （2）∵AM＝CM，

    ∴△BCM的周长＝BC＋CM＋BM＝BC＋AM＋BM＝BC＋AB＝3＋5＝8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】出租车司机王师傅某天早上营运时是在东西走向的大街上进行的，如果规定向东为正，向西为负，他这天早上所接六位乘客的行车里程()如下：

    2，+5，-4，+1，-6，-2

    (1)将最后一位乘客送到目的地时，王师傅在早上出发点的什么位置?

    (2)若汽车耗油量为，这天早上王师傅接送乘客，出租车共耗油多少升?

    (3)若出租车起步价为6元，起步里程为 (包括)，超过部分(不足按计算)每千米1．5元，王师傅这天早上共得车费多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC为等腰三角形，AC=BC，以边BC为直径的半圆与边AB，AC分别交于D，E两点，过点D作DF⊥AC，垂足为点F

    （1）判断DF与⊙O的位置关系，并证明你的结论；

    （2）若DF=3，EF=1，求弦EC的长．

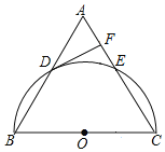
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．求证：CE＝CF；

    （2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD．

    （3）运用（1）（2）解答中所积累的经验和知识，完成下题：

    如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE="10," 求直角梯形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了奖励在数学竞赛中获奖的学生，买了若干本课外读物准备送给他们，如果每人送3本，则剩余8本；如果前面每人送5本，则最后一人得到的课外读物不足3本，设该校买了m本课外读物，有x名学生获奖，请解答下列问题：

    （1）用含x的代数式表示m；

    （2）求出该校的获奖人数及所买课外读物的本数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BC＝5，高AD、BE相交于点O，BD＝CD，且AE＝BE．

    （1）求线段AO的长；

    （2）动点P从点O出发，沿线段OA以每秒1个单位长度的速度向终点A运动，动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动，P、Q两点同时出发，当点P到达A点时，P、Q两点同时停止运动．设点P的运动时间为t秒，△POQ的面积为S，请用含t的式子表示S，并直接写出相应的t的取值范围；

    （3）在（2）的条件下，点F是直线AC上的一点且CF＝BO．是否存在t值，使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等？若存在，请直接写出符合条件的t值；若不存在，请说明理由．

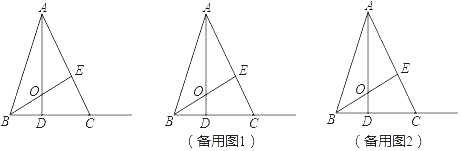
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，PA与⊙O相切于点A，过点A作AB⊥OP，垂足为C，交⊙O于点B．连接PB，AO，并延长AO交⊙O于点D，与PB的延长线交于点E．

    （1）求证：PB是⊙O的切线；

    （2）若OC=3，AC=4，求sinE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，∠A＝∠C＝90°，BE平分∠ABC，DF平分∠CDA．

    (1)求证：BE∥DF；

    (2)若∠ABC＝56°，求∠ADF的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过km/h.如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路对面车速检测仪正前方m处，过了2s后，测得小汽车与车速检测仪间距离为m，这辆小汽车超速了吗？

    查看答案和解析>>

    同步练习册答案