
【题目】如图,已知:∠AOB=90°,OC平分∠AOB,点P在射线OC上.点E在射线OA上,点F在射线OB上,且∠EPF=90°.
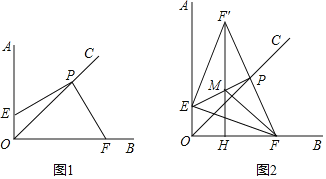
(1)如图1,求证:PE=PF;
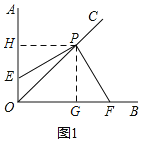
(2)如图2,作点F关于直线EP的对称点F′,过F′点作FH⊥OF于H,连接EF′,F′H与EP交于点M.连接FM,图中与∠EFM相等的角共有 个.
【答案】(1)见解析;(2)4.
【解析】
(1)过P作PG⊥OB于G,PH⊥AO于H,判定△PEH≌△PFG(AAS),即可得出PE=PF;
(2)依据轴对称的性质以及等腰直角三角形的性质,即可得到与∠EFM相等的角.
解:(1)如图1,过P作PG⊥OB于G,PH⊥AO于H,则∠PGF=∠PHE=90°,
∵OC平分∠AOB,PG⊥OB,PH⊥AO,
∴PH=PG,
∵∠AOB=∠EPF=90°,
∴∠PFG+∠PEO=180°,
又∵∠PEH+∠PEO=180°,
∴∠PEH=∠PFG,
∴△PEH≌△PFG(AAS),
∴PE=PF;
(2)由轴对称可得,∠EFM=∠EF′M,
∵F′H⊥OF,AO⊥OB,
∴AO∥F′F,
∴∠EF′M=∠AEF′,
∵∠AEF′+∠OEF=∠OFE+∠OEF=90°,
∴∠AEF′=∠OFE,
由题可得,P是FF′的中点,EF=EF′,
∴EP平分∠FEF′,
∵PE=PF,∠EPF=90°,
∴∠PEF=45°=∠PEF′,
又∵∠AOP=![]() ∠AOB=45°,且∠AEP=∠AOP+∠OPE,
∠AOB=45°,且∠AEP=∠AOP+∠OPE,
∴∠AEF′+45°=45°+∠OPE,
∴∠AEF′=∠OPE,
∴与∠EFM相等的角有4个:∠EF′M,∠AEF′,∠EFO,∠EPO.
故答案为:4.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:
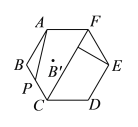
【题目】如图所示,正六边形![]() 的边长为
的边长为![]() ,点
,点![]() 从
从![]() 点出发沿
点出发沿![]() 运动至点
运动至点![]() ,点
,点![]() 是点
是点![]() 关于直线
关于直线![]() 对称的点.
对称的点.
(![]() )点
)点![]() 从点
从点![]() 运动至
运动至![]() 过程中,下列说法正确的有__________.(填序号)
过程中,下列说法正确的有__________.(填序号)
①当点![]() 运动到
运动到![]() 时,线段
时,线段![]() 长为
长为![]() .
.
②点![]() 沿直线从
沿直线从![]() 运动到
运动到![]() .
.
③点![]() 沿圆弧从
沿圆弧从![]() 运动到
运动到![]() .
.
(![]() )点
)点![]() 从点
从点![]() 运动至
运动至![]() 的过程中,点
的过程中,点![]() 到
到![]() 的距离的最小值是__________.
的距离的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了奖励在数学竞赛中获奖的学生,买了若干本课外读物准备送给他们,如果每人送3本,则剩余8本;如果前面每人送5本,则最后一人得到的课外读物不足3本,设该校买了m本课外读物,有![]() x名学生获奖,请解答下列问题:
x名学生获奖,请解答下列问题:
(1)用含x的代数式表示m;
(2)求出该校的获奖人数及所买课外读物的本数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求sinE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.
(1)求证:BE∥DF;
(2)若∠ABC=56°,求∠ADF的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,AD∥BC,要判别四边形ABCD是平行四边形,还需满足条件( )
A. ∠A+∠C=180°B. ∠B+∠D=180°
C. ∠A+∠B=180°D. ∠A+∠D=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com