
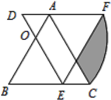
【题目】△ABC为等边三角形,点O为AB边上一点,且BO=2AO=4,将△ABC绕点O逆时针旋转60°得△DEF,则图中阴影部分的面积为______.
【答案】![]()
【解析】
连接OC,OF,作CG⊥AB,OM⊥BC, FH⊥AB的延长线于点H.根据三线合一求出BG= AG=3,进而求得OG,由三角函数求得CG,解直角三角形OGC得出OC长,再由面积公式分别求得![]() ,
,![]() =
=![]() ,
,![]() ,
,![]() ,利用
,利用![]() =
=![]() +
+ ![]() +
+![]() -
-![]() -
-![]() 求得答案即可.
求得答案即可.
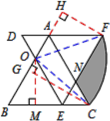
连接OC,OF,作CG⊥AB,OM⊥BC, FH⊥AB的延长线于点H.
∵BO=2AO=4,
∴AO=2,AB=6,
∵△ABC为等边三角形,CG⊥AB,
∴BG= AG=![]() AB=3,CG=BC·sin60°=
AB=3,CG=BC·sin60°= ![]() ,
,
∴OG=3-2=1,
Rt△OGC中,OG=1,CG=![]() ,
,
∴OC=![]() =
=![]() ,
,
易证△NEC,△AOD,△BOE为等边三角形,四边形AOEF为等腰梯形,
∴AF=OE=4,CE=AO=2,OM=HF=4×sin60°=![]() ,
,
∵′![]() =
=  =
= ![]() ,
, ![]() =
=![]() =
= ![]() =
= ![]() ,
,
![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,
,
∴![]() =
=![]() +
+ ![]() +
+![]() -
-![]() -
-![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
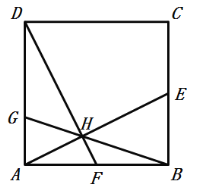
【题目】如图,正方形ABCD的边长为10,点E,F分别为BC,AB边的中点.连接AE、DF,两线交于点H,连接BH并延长,交边AD于点G.下列结论:①△ABE≌△DAF,②cos∠BAE=![]() ,③
,③![]() :S四边形CDHE=1:11,④AG=
:S四边形CDHE=1:11,④AG=![]() 其中正确的是( )
其中正确的是( )
A.①③④B.①②③
C.①④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
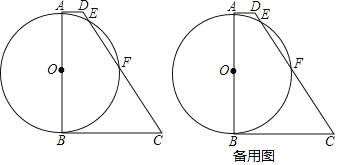
【题目】如图,已知在四边形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O交边DC于E、F两点,AD=1,BC=5,设⊙O的半径长为r.
(1)联结OF,当OF∥BC时,求⊙O的半径长;
(2)过点O作OH⊥EF,垂足为点H,设OH=y,试用r的代数式表示y;
(3)设点G为DC的中点,联结OG、OD,△ODG是否能成为等腰三角形?如果能,试求出r的值;如不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
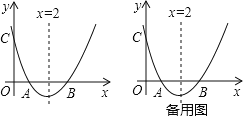
(1)求抛物线的函数表达式;
(2)设D为抛物线的顶点,连接DA、DB,试判断△ABD的形状,并说明理由;
(3)设P为对称轴上一动点,要使PC﹣PB的值最大,求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间,经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| … | 190 | 200 | 210 | 220 | … |
| … | 65 | 60 | 55 | 50 | … |
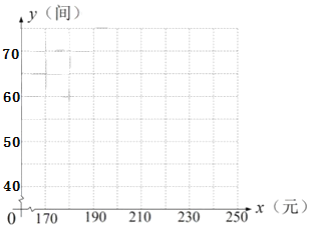
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)求![]() 关于
关于![]() 的函数表达式、并写出自变量
的函数表达式、并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为![]() (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
(元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,单位长度为1的网格坐标系中,一次函数 ![]() 与坐标轴交于A、B两点,反比例函数
与坐标轴交于A、B两点,反比例函数![]() (x>0)经过一次函数上一点C(2,a).
(x>0)经过一次函数上一点C(2,a).
(1)求反比例函数解析式,并用平滑曲线描绘出反比例函数图像;
(2)依据图像直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)若反比例函数![]() 与一次函数
与一次函数![]() 交于C、D两点,使用直尺与2B铅笔构造以C、D为顶点的矩形,且使得矩形的面积为10.
交于C、D两点,使用直尺与2B铅笔构造以C、D为顶点的矩形,且使得矩形的面积为10.
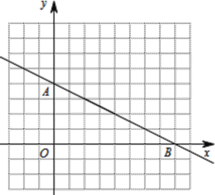

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AC为直径,点D为弧ACB的中点,过点D的切线与BC的延长线交于点E.
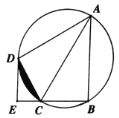
(1)用尺规作图作出圆心O;(保留作图痕迹,不写作法);
(2)求证:DE⊥BC;
(3)若OC=2CE=4,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2![]() x+m=0有两个不相等的实数根.
x+m=0有两个不相等的实数根.
(1)求实数m的最大整数值;
(2)在(1)的条件下,方程的实数根是![]() 、
、![]() ,求代数式
,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
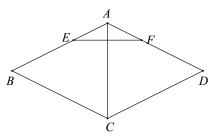
【题目】如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,BE=DF,连接EF.
(1)求证:AC⊥EF;
(2)延长EF交CD的延长线于点G,连接BD交AC于点O,若BD=4,tanG=![]() ,求AO的长.
,求AO的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com