
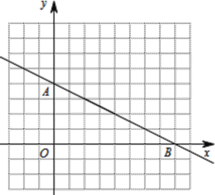
【题目】如图,单位长度为1的网格坐标系中,一次函数 ![]() 与坐标轴交于A、B两点,反比例函数
与坐标轴交于A、B两点,反比例函数![]() (x>0)经过一次函数上一点C(2,a).
(x>0)经过一次函数上一点C(2,a).
(1)求反比例函数解析式,并用平滑曲线描绘出反比例函数图像;
(2)依据图像直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)若反比例函数![]() 与一次函数
与一次函数![]() 交于C、D两点,使用直尺与2B铅笔构造以C、D为顶点的矩形,且使得矩形的面积为10.
交于C、D两点,使用直尺与2B铅笔构造以C、D为顶点的矩形,且使得矩形的面积为10.

【答案】(1)图详见解析,![]() ;(2)
;(2)![]() ;(3)详见解析
;(3)详见解析
【解析】
(1)读出A,B两点的坐标,将A,B坐标代入直线解析式,求出直线的解析式,然后求出点C的坐标,将C点坐标代入![]() ,利用待定系数法即可求出反比例函数的解析式,然后描点画出反比例函数的图象;
,利用待定系数法即可求出反比例函数的解析式,然后描点画出反比例函数的图象;
(2)结合图象读出不等式的解集;
(3)根据矩形满足的两个条件画出符合要求的两个矩形即可.
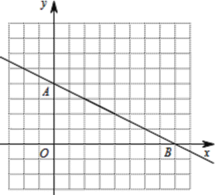
解(1)由图知点A坐标为(0,4),点B的坐标为(8,0),一次函数![]() 经过A、B两点,
经过A、B两点,
∴![]() ,
,
解得: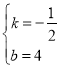 ,
,
∴一次函数解析式为:![]() ,
,
∵![]() 经过点C (2,a),
经过点C (2,a),
∴![]() ,∴点C坐标为(2,3),
,∴点C坐标为(2,3),
∵反比例函数![]() 经过点C(2,3),
经过点C(2,3),
∴![]() ,
,
∴反比例函数解析式为:![]() ;
;
(2)描绘出反比例函数![]() (x>0)的图像如下:
(x>0)的图像如下:
依据函数图像可得,当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() ;
;
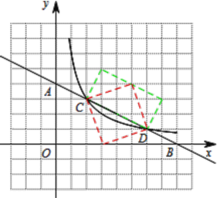
(3)由图像可知点C的坐标为(2,3),点D的坐标为(6,1),
依据勾股定理可得CD=![]() =
=![]() ,已知矩形面积为10的情况下,分类讨论:
,已知矩形面积为10的情况下,分类讨论:
若以CD为边构造矩形,则矩形的另一边为![]() ;若以CD为对角线的情况下构造矩形,此时矩形为正方形,得其边长为
;若以CD为对角线的情况下构造矩形,此时矩形为正方形,得其边长为![]() ,故构造符合题意的矩形共有两个,如图所示.
,故构造符合题意的矩形共有两个,如图所示.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
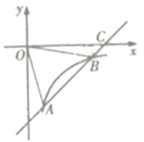
【题目】如图,已知一次函数y= kx +b的图象交反比例函数![]() 的图象于点A(2,-4)和点B(h,-2),交x轴于点C.
的图象于点A(2,-4)和点B(h,-2),交x轴于点C.
(1)求这两个函数的解析式;
(2)连接QA、OB.求△AOB的面积;
(3)请直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
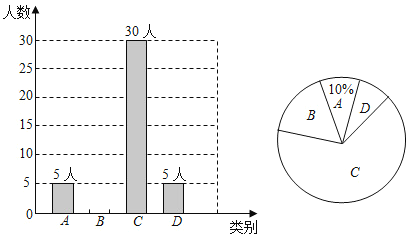
【题目】央视“经典咏流传”开播以来受到社会广泛关注,金昌市某校就学生喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图,请你根据统计图所提供的信息,解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”
(1)此次抽样调查,共调查了 名学生;
(2)将图1中的条形统计图补充完整;
(3)图2中,C部分所在扇形的圆心角为 度;
(4)若该校共有学生1800人,估计该校学生中D类有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
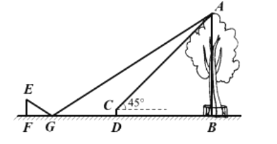
【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
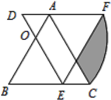
【题目】△ABC为等边三角形,点O为AB边上一点,且BO=2AO=4,将△ABC绕点O逆时针旋转60°得△DEF,则图中阴影部分的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了考查学生的综合素质,某市决定:九年级毕业生统一参加中考实验操作考试,根据今年的实际情况,中考实验操作考试科目为:![]() (物理)、
(物理)、![]() (化学)、
(化学)、![]() (生物),每科试题各为
(生物),每科试题各为![]() 道,考生随机抽取其中
道,考生随机抽取其中![]() 道进行考试.小明和小丽是某校九年级学生,需参加实验考试.
道进行考试.小明和小丽是某校九年级学生,需参加实验考试.
(1)小明抽到化学实验的概率为 ;
(2)若只从考试科目考虑,小明和小丽抽到不同科目的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下统计图:

(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为___________度
(2)请补充完整下面的成绩统计分析表:
平均数 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 |
|
乙组 | 1.36 |
|
(3)你认为那组成绩较好?从以上信息中写出两条支持你的选择
(4)从甲、乙两组得9分的学生中抽取两人参加市级比赛,求这两人来自不同组的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=AB·AD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则∠DAB=_________.
(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长?

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为
与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为![]() (
(![]() ).
).
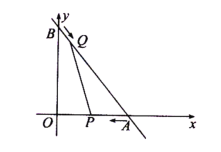
(1)写出A、B两点的坐标;
(2)设![]() 的面积为S,试求出S与t之间的函数关系式,并求出当t为何值时,
的面积为S,试求出S与t之间的函数关系式,并求出当t为何值时,![]() 的面积最大;
的面积最大;
(3)当t为何值时,以点A,P,Q为顶点的三角形与![]() 相似?并直接写出此时点Q的坐标.
相似?并直接写出此时点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com