
【题目】如图,直线![]() 与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为
与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为![]() (
(![]() ).
).
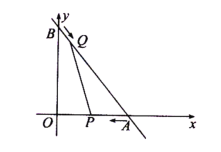
(1)写出A、B两点的坐标;
(2)设![]() 的面积为S,试求出S与t之间的函数关系式,并求出当t为何值时,
的面积为S,试求出S与t之间的函数关系式,并求出当t为何值时,![]() 的面积最大;
的面积最大;
(3)当t为何值时,以点A,P,Q为顶点的三角形与![]() 相似?并直接写出此时点Q的坐标.
相似?并直接写出此时点Q的坐标.
【答案】(1)A(6,0),B(0,8);(2)![]() ,当t=3s时,
,当t=3s时,![]() 取得最大值
取得最大值![]() ;(3)当t=
;(3)当t=![]() s时,△APQ与△AOB相似.此时点Q的坐标为(
s时,△APQ与△AOB相似.此时点Q的坐标为(![]() ,
,![]() ).
).
【解析】
(1)分别令y=0,x=0求解即可得到点A、B的坐标
(2)利用勾股定理列式求出AB,然后表示AP、AQ,再利用∠OAB的正弦求出点Q到AP的距离,然后利用三角形的面积列式整理即可
(3)根据相似三角形对应角相等,分∠APQ=90°和∠AQP=90°两种情况,利用∠OAB的余弦列式计算即可得解
解:(1)令y=0,则﹣![]() x+8=0,
x+8=0,
解得x=6,
x=0时,y=8,
∴OA=6,OB=8,
∴点A(6,0),B(0,8);
(2)在Rt△AOB中,由勾股定理得,AB=![]() =
=![]() =10,
=10,
∵点P的速度是每秒2个单位,点Q的速度是每秒1个单位,
∴AP=2t,
AQ=AB﹣BQ=10﹣t,
∴点Q到AP的距离为AQsin∠OAB=(10﹣t)×![]() =
=![]() (10﹣t),
(10﹣t),
∴△AQP的面积S=![]() ×2t×
×2t×![]() (10﹣t)=﹣
(10﹣t)=﹣![]() (t2﹣10t)=﹣
(t2﹣10t)=﹣![]() (t﹣5)2+20,
(t﹣5)2+20,
∵﹣![]() <0,0<t≤3,
<0,0<t≤3,
∴当t=3时,△AQP的面积最大,S最大=﹣![]() (3﹣5)2+20=
(3﹣5)2+20=![]() ;
;
(3)若∠APQ=90°,则cos∠OAB=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() ,
,
若∠AQP=90°,则cos∠OAB=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() ,
,
∵0<t≤3,
∴t的值为![]() ,
,
此时,OP=6﹣2×![]() =
=![]() ,
,
PQ=APtan∠OAB=(2×![]() )×
)×![]() =
=![]() ,
,
∴点Q的坐标为(![]() ,
,![]() ),
),
综上所述,t=![]() 秒时,以点A,P,Q为顶点的三角形与△ABO相似,此时点Q的坐标为(
秒时,以点A,P,Q为顶点的三角形与△ABO相似,此时点Q的坐标为(![]() ,
,![]() )
)


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
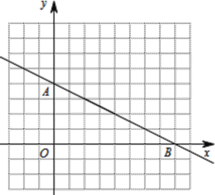
【题目】如图,单位长度为1的网格坐标系中,一次函数 ![]() 与坐标轴交于A、B两点,反比例函数
与坐标轴交于A、B两点,反比例函数![]() (x>0)经过一次函数上一点C(2,a).
(x>0)经过一次函数上一点C(2,a).
(1)求反比例函数解析式,并用平滑曲线描绘出反比例函数图像;
(2)依据图像直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)若反比例函数![]() 与一次函数
与一次函数![]() 交于C、D两点,使用直尺与2B铅笔构造以C、D为顶点的矩形,且使得矩形的面积为10.
交于C、D两点,使用直尺与2B铅笔构造以C、D为顶点的矩形,且使得矩形的面积为10.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将曲线c1:y=![]() (x>0)绕原点O逆时针旋转60°得到曲线c2,A为直线y=
(x>0)绕原点O逆时针旋转60°得到曲线c2,A为直线y=![]() x上一点,P为曲线c2上一点,PA=PO,且△PAO的面积为6
x上一点,P为曲线c2上一点,PA=PO,且△PAO的面积为6![]() ,直线y=
,直线y=![]() x交曲线c1于点B,则OB的长( )
x交曲线c1于点B,则OB的长( )

A.2![]() B.5C.3
B.5C.3![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场秋季计划购进一批进价为每件40元的![]() 恤进行销售.
恤进行销售.
(1)根据销售经验,应季销售时,若每件![]() 恤的售价为60元,可售出400件;若每件
恤的售价为60元,可售出400件;若每件![]() 恤的售价每提高1元,销售量相应减少10件.
恤的售价每提高1元,销售量相应减少10件.
①假设每件![]() 恤的售价提高
恤的售价提高![]() 元,那么销售每件
元,那么销售每件![]() 恤所获得的利润是 元,销售量是 件(用含
恤所获得的利润是 元,销售量是 件(用含![]() 的代数式表示);
的代数式表示);
②设应季销售利润为![]() 元,请写
元,请写![]() 与
与![]() 的函数关系式;并求出应季销售利润为8000元时每件
的函数关系式;并求出应季销售利润为8000元时每件![]() 恤的售价.
恤的售价.
(2)根据销售经验,过季处理时,若每件![]() 恤的售价定为30元亏本销售,可售出50件;若每件
恤的售价定为30元亏本销售,可售出50件;若每件![]() 恤的售价每降低1元,销售量相应增加5条.
恤的售价每降低1元,销售量相应增加5条.
①若剩余100件![]() 恤需要处理,经过降价处理后还是无法销售的只能积压在仓库,损失本金;若使亏损金额最小,每件
恤需要处理,经过降价处理后还是无法销售的只能积压在仓库,损失本金;若使亏损金额最小,每件![]() 恤的售价应是多少元?
恤的售价应是多少元?
②若过季需要处理的![]() 恤共
恤共![]() 件,且
件,且![]() ,季亏损金额最小是 元(用含
,季亏损金额最小是 元(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
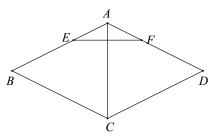
【题目】如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,BE=DF,连接EF.
(1)求证:AC⊥EF;
(2)延长EF交CD的延长线于点G,连接BD交AC于点O,若BD=4,tanG=![]() ,求AO的长.
,求AO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
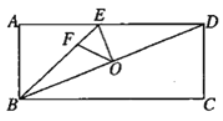
【题目】如图,O为矩形ABCD的对角线BD的中点,点E在AD上,连接EB、EO,BD平分∠EBC,点F在BE上,tan∠OFE=tan∠ABD,若AE=3EF,CD=3,则OD的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
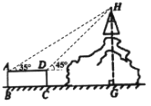
【题目】如图,山上有一座高塔,山脚下有一圆柱形建筑物平台,高塔及山的剖面与圆柱形建筑物平台的剖面ABCD在同一平面上,在点A处测得塔顶H的仰角为35°,在点D处测得塔顶H的仰角为45°,又测得圆柱形建筑物的上底面直径AD为6m,高CD为2.8m,则塔顶端H到地面的高度HG为( )
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
A.10.8mB.14mC.16.8mD.29.8m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com