
【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求一次函数的解析式;
(2)判断点C(4,-2)是否在该一次函数的图象上,说明理由;
(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.

【答案】(1)y=-x+3;(2)不在,理由见解析;(3)3
【解析】(1)首先求得B的坐标,然后利用待定系数法即可求得函数的解析式;
(2)把C的坐标代入一次函数的解析式进行检验即可;
(3)首先求得D的坐标,然后利用三角形的面积公式求解.
解:(1)在y=2x中,令x=1,得y=2,则点B的坐标是(1,2),
设一次函数的解析式是y=kx+b(k≠0),
则![]() 解得
解得![]()
故一次函数的解析式是y=-x+3.
(2)点C(4,-2)不在该一次函数的图象上.
理由:对于y=-x+3,当x=4时,y=-1≠-2,
所以点C(4,-2)不在该函数的图象上.
(3)在y=-x+3中,令y=0,得x=3,则点D的坐标是(3,0),
则S△BOD=![]() ×OD×2=
×OD×2=![]() ×3×2=3.
×3×2=3.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】一部记录片播放了关于地震的资料及一个有关地震预测的讨论,一位专家指出:“在未来20年,A城市发生地震的机会是三分之二”
对这位专家的陈述下面有四个推断:
①![]() ×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
②![]() 大于50%,所以未来20年,A城市一定发生地震;
大于50%,所以未来20年,A城市一定发生地震;
③在未来20年,A城市发生地震的可能性大于不发生地震的可能性;
④不能确定在未来20年,A城市是否会发生地震;
其中合理的是( )
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
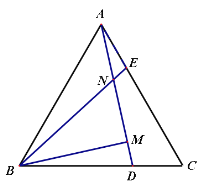
【题目】已知:△ABC为等边三角形,点D、E分别在BC和AC上,并且CD=AE,连接AD、BE相交于点N,过点B作BM⊥AD于点M.
(1)求证:BE=AD
(2)若NE=2,MN=5,求AD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,sinA= ![]() ,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF.
,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF. 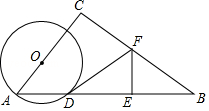
(1)求证:DF为⊙O的切线;
(2)若AO=x,DF=y,求y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图所示,大正方形固定不动,把小正方形以1厘米∕秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.完成下列问题:
(1)平移1.5秒时,S为________平方厘米;
(2)当2≤t≤4时,求小正方形的一条对角线扫过的图形的面积;
(3)当S为2平方厘米时,求小正方形平移的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索三角形的内角与外角平分线(三角形的外角是三角形的一边与另一边的延长线所组成的角):
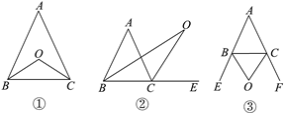
(1)如图①,在△ABC中,BO平分∠ABC,CO平分∠ACB,若∠A=50°,则∠BOC=________;此时∠A与∠BOC有怎样的关系?试说明理由.
(2)如图②,BO平分∠ABC,CO平分∠ACE,若∠A=50°,则∠BOC=________;此时∠A与∠BOC有怎样的关系?试说明理由.
(3)如图③,△ABC的外角∠CBE,∠BCF的平分线BO,CO相交于点O,若∠A=50°,则∠BOC=______;此时∠A与∠BOC有怎样的关系?(不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1菱形ABCD,∠ABC=60°,边长为 3,在菱形内作等边三角形△AEF,边长为2 ![]() ,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2
,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2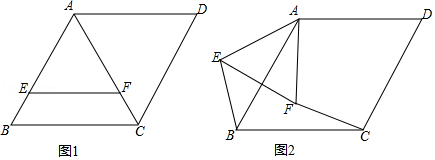
(1)在图2中证明BE=CF;
(2)若∠BAE=45°,求CF的长度;
(3)当CF= ![]() 时,直接写出旋转角α的度数.
时,直接写出旋转角α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,正方形OABC的面积为16,点D的坐标为(0,3).将直线BD沿y轴向下平移d个单位得到直线l(0<d≤4).
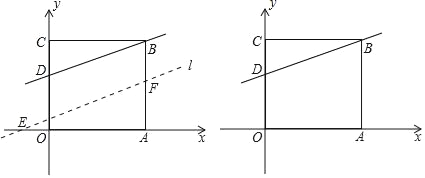
(1)则点B的坐标为 ;
(2)当d=1时,求直线l的函数表达式;
(3)设直线l与x轴相交于点E,与边AB相交于点F,若CE=CF,求d的值并直接写出此时∠ECF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com