
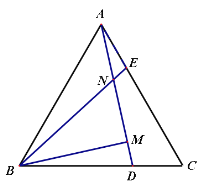
【题目】已知:△ABC为等边三角形,点D、E分别在BC和AC上,并且CD=AE,连接AD、BE相交于点N,过点B作BM⊥AD于点M.
(1)求证:BE=AD
(2)若NE=2,MN=5,求AD的长
【答案】(1)证明见解析;(2)AD=12.
【解析】
(1)根据等边三角形的性质可得,AB=AC,∠BAE=∠C,然后利用SAS即可证得;
(2)根据全等三角形的性质,以及三角形的外角的性质求得∠BNM=60![]() ,然后根据直角三角形的性质求得BN的长,则AB即可求得,根据AD=BE即可求得.
,然后根据直角三角形的性质求得BN的长,则AB即可求得,根据AD=BE即可求得.
(1) 证明:∵△ABC为等边三角形,
∴∠BAC=∠C=60°AB=CA ∠BAE=∠C,AE=CD,
∴△ABE≌△CAD
∴BE=AD
(2) ∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BND=∠CAD +∠BAD=∠BAC=60°,
∴∠MBN=30°,
∴BN=2MN=2×5=10,
∴BE=12,
∴AD=12,


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】A、B两地的距离是80千米,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍,已知小汽车比公共汽车迟20分钟到达B地,求两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形是将正三角形按一定规律排列,第 1 个图形中所有正三角形的个数有 1 个,第 2 个图形中所有正三角形的个数有 5 个,第 3 个图形中所有正三角形的个数有 17 个,则第 5 个图形中所有正三角形的个数有( )
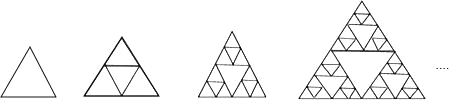
A. 160 B. 161 C. 162 D. 163
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小兰:“小红,你上周买的笔和笔记本的价格是多少啊?”小红:“哦,…,我忘了!只记得先后买了两次,第一次买了5支笔和10本笔记本共花了42元钱,第二次买了10支笔和5本笔记本共花了30元钱.”请根据小红与小兰的对话,求得小红所买的笔和笔记本的价格分别是( )
A. 0.8元/支,2.6元/本 B. 1.2元/支,3.6元/本
C. 1.2元/支,2.6元/本 D. 0.8元/支,3.6元/本
查看答案和解析>>
科目:初中数学 来源: 题型:
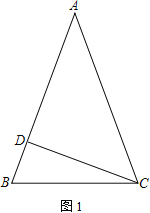
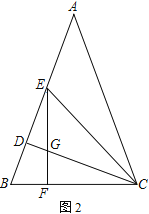
【题目】在△ABC中,AB=AC,CD为AB边上的高
(1) 如图1,求证:∠BAC=2∠BCD
(2) 如图2,∠ACD的平分线CE交AB于E,过E作EF⊥BC于F,EF与CD交于点G.若ED=m,BD=n,请用含有m、n的代数式表示△EGC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:
地点 | 票价 |
历史博物馆 | 10元/人 |
民俗展览馆 | 20元/人 |
(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求一次函数的解析式;
(2)判断点C(4,-2)是否在该一次函数的图象上,说明理由;
(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
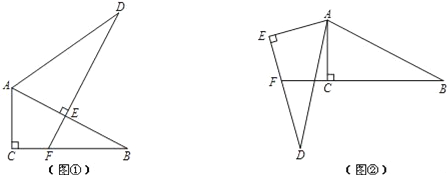
【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.
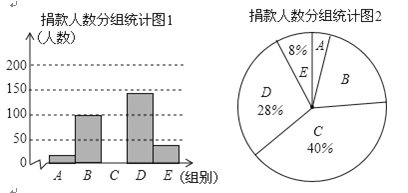
被调查的捐款人数分组统计表:
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | ______ |
D | 30≤x<40 | ______ |
E | 40≤x | ______ |
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com