
【题目】探索三角形的内角与外角平分线(三角形的外角是三角形的一边与另一边的延长线所组成的角):
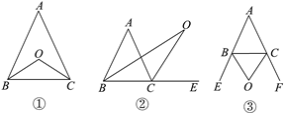
(1)如图①,在△ABC中,BO平分∠ABC,CO平分∠ACB,若∠A=50°,则∠BOC=________;此时∠A与∠BOC有怎样的关系?试说明理由.
(2)如图②,BO平分∠ABC,CO平分∠ACE,若∠A=50°,则∠BOC=________;此时∠A与∠BOC有怎样的关系?试说明理由.
(3)如图③,△ABC的外角∠CBE,∠BCF的平分线BO,CO相交于点O,若∠A=50°,则∠BOC=______;此时∠A与∠BOC有怎样的关系?(不需说明理由)
【答案】(1)115°,∠BOC=90°+![]() ∠A,.理由见解析;(2)25°,∠BOC=
∠A,.理由见解析;(2)25°,∠BOC=![]() ∠A,理由见解析;(3)65°,∠BOC=90°-
∠A,理由见解析;(3)65°,∠BOC=90°-![]() ∠A.
∠A.
【解析】
(1)根据三角形内角和定理得到∠BOC=180°-∠OBC-∠OCB,则2∠BOC=360°-2∠OBC-2∠OCB,再根据角平分线的定义得∠ABC=2∠OBC,∠ACB=2∠OCB,则2∠BOC=360°-∠ABC-∠ACB,易得∠BOC=90°+![]() ∠A.
∠A.
(2)根据角平分线的定义得∠ACE=2∠OCE,∠ABC=2∠OBC,由三角形外角的性质有∠OCE=∠BOC+∠OBC,∠ACE=∠ABC+∠A,则2∠BOC+2∠OBC=∠ABC+∠A,即可得到∠BOC=![]() ∠A;
∠A;
(3)根据三角形内角和定理和外角性质可得到∠BOC=90°-![]() ∠A.
∠A.
(1)115° ∠BOC=90°+![]() ∠A.理由如下:
∠A.理由如下:
∵∠BOC=180°-∠OBC-∠OCB,
∴2∠BOC=360°-2∠OBC-2∠OCB.
而BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴2∠BOC=360°-(∠ABC+∠ACB).
∵∠ABC+∠ACB=180°-∠A,
∴2∠BOC=180°+∠A,
∴∠BOC=90°+![]() ∠A.
∠A.
(2)25° ∠BOC=![]() ∠A.理由如下:
∠A.理由如下:
∵CO平分∠ACE,
∴∠ACE=2∠OCE.
∵∠OCE=∠OBC+∠BOC,
∠ACE=∠ABC+∠A,
∴∠ABC+∠A=2∠OBC+2∠BOC.
∵BO平分∠ABC,∴∠ABC=2∠OBC,
∴2∠OBC+∠A=2∠OBC+2∠BOC,
∴∠A=2∠BOC,即∠BOC=![]() ∠A.
∠A.
(3)65° ∠BOC=90°-![]() ∠A.
∠A.


科目:初中数学 来源: 题型:
【题目】为响应珠海环保城市建设,我市某污水处理公司不断改进污水处理设备,新设备每小时处理污水量是原系统的1.5倍,原来处理1200m3污水所用的时间比现在多用10小时.
(1)原来每小时处理污水量是多少m2?
(2)若用新设备处理污水960m3,需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,CD为AB边上的高
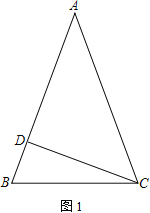
(1) 如图1,求证:∠BAC=2∠BCD
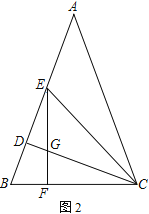
(2) 如图2,∠ACD的平分线CE交AB于E,过E作EF⊥BC于F,EF与CD交于点G.若ED=m,BD=n,请用含有m、n的代数式表示△EGC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求一次函数的解析式;
(2)判断点C(4,-2)是否在该一次函数的图象上,说明理由;
(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知A( ![]() ,y1),B(2,y2)为反比例函数y=
,y1),B(2,y2)为反比例函数y= ![]() 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )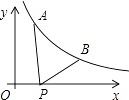
A.( ![]() ,0)
,0)
B.(1,0)
C.( ![]() ,0)
,0)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
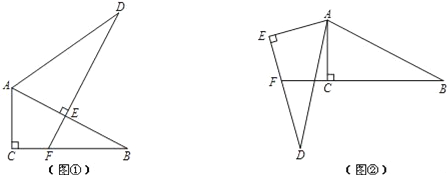
【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
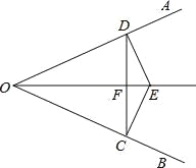
【题目】如图,已知:E 是∠AOB 的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接 CD,且交 OE 于点F.
(1)求证:OD=OC;
(2)求证:OE 是 CD 的垂直平分线;
(3)若∠AOB=60°,请你探究 OE,EF 之间有什么数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣12a2b2c)(﹣![]() abc2)2=___________;
abc2)2=___________;
(2)(3a2b﹣4ab2﹣5ab﹣1)(﹣2ab2)=___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com