
【题目】计算:
(1)(﹣12a2b2c)(﹣![]() abc2)2=___________;
abc2)2=___________;
(2)(3a2b﹣4ab2﹣5ab﹣1)(﹣2ab2)=___________.
【答案】(1)﹣![]() a4b4c5 (2)﹣6a3b3+8a2b4+10a2b3+2ab2
a4b4c5 (2)﹣6a3b3+8a2b4+10a2b3+2ab2
【解析】
试题(1)先根据积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘;单项式乘单项式,把他们的系数,相同字母的幂分别相乘,其余字母连同他的指数不变,作为积的因式的法则计算;
(2)根据单项式乘多项式,先用单项式去乘多项式的每一项,再把所得的积相加的法则计算即可.
解:(1)(﹣12a2b2c)(﹣![]() abc2)2,
abc2)2,
=(﹣12a2b2c)![]() ,
,
=﹣![]() ;
;
故答案为:﹣![]() a4b4c5;
a4b4c5;
(2)(3a2b﹣4ab2﹣5ab﹣1)(﹣2ab2),
=3a2b(﹣2ab2)﹣4ab2(﹣2ab2)﹣5ab(﹣2ab2)﹣1(﹣2ab2),
=﹣6a3b3+8a2b4+10a2b3+2ab2.
故答案为:﹣6a3b3+8a2b4+10a2b3+2ab2.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】一部记录片播放了关于地震的资料及一个有关地震预测的讨论,一位专家指出:“在未来20年,A城市发生地震的机会是三分之二”
对这位专家的陈述下面有四个推断:
①![]() ×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
②![]() 大于50%,所以未来20年,A城市一定发生地震;
大于50%,所以未来20年,A城市一定发生地震;
③在未来20年,A城市发生地震的可能性大于不发生地震的可能性;
④不能确定在未来20年,A城市是否会发生地震;
其中合理的是( )
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索三角形的内角与外角平分线(三角形的外角是三角形的一边与另一边的延长线所组成的角):
(1)如图①,在△ABC中,BO平分∠ABC,CO平分∠ACB,若∠A=50°,则∠BOC=________;此时∠A与∠BOC有怎样的关系?试说明理由.
(2)如图②,BO平分∠ABC,CO平分∠ACE,若∠A=50°,则∠BOC=________;此时∠A与∠BOC有怎样的关系?试说明理由.
(3)如图③,△ABC的外角∠CBE,∠BCF的平分线BO,CO相交于点O,若∠A=50°,则∠BOC=______;此时∠A与∠BOC有怎样的关系?(不需说明理由)
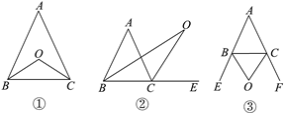
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1菱形ABCD,∠ABC=60°,边长为 3,在菱形内作等边三角形△AEF,边长为2 ![]() ,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2
,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2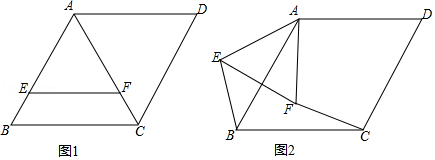
(1)在图2中证明BE=CF;
(2)若∠BAE=45°,求CF的长度;
(3)当CF= ![]() 时,直接写出旋转角α的度数.
时,直接写出旋转角α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平整的地面上,10个完全相同的棱长为8cm的小正方体堆成一个几何体.
(1)在下面的网格中画出从左面看和从上面看的形状图.

(2)如果在这个几何体的表面(不含底面)喷上黄色的漆,则这个几何体喷漆的面积是多少cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣8,0),点P的坐标为 ![]() ,直线y=
,直线y= ![]() x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.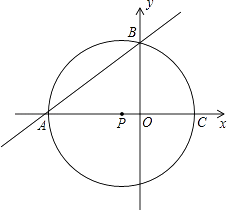
(1)判断点B是否在⊙P上?说明理由.
(2)求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.
(3)⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,正方形OABC的面积为16,点D的坐标为(0,3).将直线BD沿y轴向下平移d个单位得到直线l(0<d≤4).
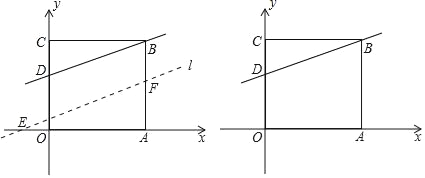
(1)则点B的坐标为 ;
(2)当d=1时,求直线l的函数表达式;
(3)设直线l与x轴相交于点E,与边AB相交于点F,若CE=CF,求d的值并直接写出此时∠ECF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com