
����Ŀ����֪������y��ax2��2amx��am2��2m��4�Ķ���P��һ����ֱ��l�ϣ�
��1��ֱ��д��ֱ��l�Ľ���ʽ��
��2��������Ψһ��ʵ��m��ʹ�����߾���ԭ�㣮
�����ʱ��a��m��ֵ��
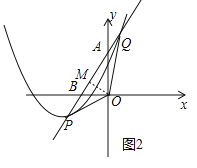
�������ߵĶԳ�����x�ύ�ڵ�A��BΪ��������һ���㣬��OA��OBΪ������OACB������C���������ϣ���B�����꣮
��3����������ֱ��l����һ������Q����a��1��ֱ��д����OPQ�������ֵ��ȡֵ��Χ��
���𰸡���1��y=2x+4��2����m=-4����B��-2��-3����3��![]()
�������������������1�������䷽������������꣬���ɽ�����⣮
��2���������߾���ԭ�㣬����x=0ʱ��y=0����am2+2m+4=0����Ϊʵ��mΨһ��������=0���õ�4��16a=0���ɵ�a=![]() ��m=��4��
��m=��4��
����ͼ1�У�����ƽ���ı��ε����ʣ���֪��B�ĺ�����Ϊ��2���ɴ˿��������B���꣮
��3����ͼ2�У�ֱ��y=2x+4��x�ύ�ڵ�B����2��0������y���ڵ�A��0��4������OM��AB��M����![]() OAOB=
OAOB=![]() ABOM�����OM�����÷�����
ABOM�����OM�����÷�����![]() ���ɵ�P��m��m+2����Q��m+2��2m+8�������PQ�ij����ɽ�����⣮
���ɵ�P��m��m+2����Q��m+2��2m+8�������PQ�ij����ɽ�����⣮
����������⣺��1����y=ax2��2amx+am2+2m+4=a��x��m��2+2m+4��������P����Ϊ��m��2m+4����������P��ֱ��y=2x+4�ϣ�
��2���١������߾���ԭ�㣬��x=0ʱ��y=0����am2+2m+4=0����ʵ��mΨһ�����=0����4��16a=0����a=![]() ��m=��4��
��m=��4��
����ͼ1�У����ı���OACB��ƽ���ı��Σ���OA��BC��OA=BC=4����BC��x�ᣬA����4��0�������ݶԳ��Կ�֪��B��C���ڶԳ���Գƣ�����B�ĺ�����Ϊ��2��y=![]() ��x+4��2��4����x=��2ʱ��y=��3������B����Ϊ����2����3����
��x+4��2��4����x=��2ʱ��y=��3������B����Ϊ����2����3����
��3����ͼ2�У���ֱ��y=2x+4��x�ύ�ڵ�B����2��0������y���ڵ�A��0��4������OM��AB��M����OB=2��OA=4����AB=![]() =
=![]() ����
����![]() OAOB=
OAOB=![]() ABOM����OM=/span>
ABOM����OM=/span>![]() ����a=1���������ߵĽ���ʽΪy=x2��2mx+m2+2m+4����
����a=1���������ߵĽ���ʽΪy=x2��2mx+m2+2m+4����![]() ����ȥy��x2����2m+2��x+m��m+2��=0�����x=m��m=2����
����ȥy��x2����2m+2��x+m��m+2��=0�����x=m��m=2����![]() ��
��![]() ����P��m��m+2����Q��m+2��2m+8������PQ=
����P��m��m+2����Q��m+2��2m+8������PQ=![]() =
=![]() ����S��POQ=
����S��POQ=![]() PQOM=
PQOM=![]() ��
��![]() ��
��![]() =
=![]() ��
��



 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��ֱ�������Σ��ӳ�AB����E��ʹBE=BC����BC��ȡһ��F��ʹBF=AB������EF����ABC��ת�������FBE�غϣ���ش�
(1)��ת�����ǵ�____��
(2)��ת��____�ȣ�
(3) AC��EF�Ĺ�ϵΪ_________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ������Ʒ������ÿ��5Ԫ�ļ۸����ۣ�ÿ��������3���������ÿ��6Ԫ�ļ۸����ۣ�ÿ��������2������ٶ�ÿ�����ۼ���![]() ��������۸�
��������۸�![]() ��Ԫ/����֮������һ�κ�����ϵ��
��Ԫ/����֮������һ�κ�����ϵ��
(1)����y��x֮��ĺ�����ϵʽ��
(2)��������Ʒ����ʱ����Ϊ4Ԫ�������ۼ۸�Ϊ����ʱ������ʹÿ�µ������ÿ�µ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OE�ѡ�AOC�ֳ������֣��ҡ�AOE�á�EOC��2��5
(1)��ͼ������BOD��70�㣬���BOE
(2)��ͼ����OFƽ�֡�BOE����BOF����AOC��10�㣬���EOF

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���ڽ�Ϊ60�������� ABCD�У�AB��2����P��ÿ��1cm���ٶȴӵ�A��������AD��DC��·���˶�������Cֹͣ������P ��PQ��BD��PQ ���AD�����CD�����ڵ�Q����ABQ�����y��cm2�����P ���˶�ʱ��x���룩�ĺ���ͼ������ǣ� ��

A. B.
B. C.
C.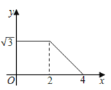 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y��kx��b��ͼ��ƽ����y����2x��1���ҹ��㣨2����1������
��1�����һ�κ����Ľ���ʽ��
��2��������һ�κ�����ͼ����ͼ��ش𣺵�xȡ��ֵʱ����ʽ kx��b��3��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�ĶԽ���AC��BD���ڵ�O��AEƽ�֡�BAD��BC�ڵ�E���ҡ�ADC��60�㣬AB��![]() BC������OE.���н��ۣ�
BC������OE.���н��ۣ�
�١�CAD��30�㣻��SABCD��AB��AC����OB��AB����OE��![]() BC�������Ľ�����______��(�����)
BC�������Ľ�����______��(�����)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC�У�AB=AC����D��BC�ϣ���AD=AE.
(1)����BAC=90��,��BAD=30�������EDC�Ķ���?
(2)����BAC=a(a>30��),��BAD=30�������EDC�Ķ���?
(3)�����EDC���BAD��������ϵ?(����֤��)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com