
【题目】如图,在一个内角为60°的菱形 ABCD中,AB=2,点P以每秒1cm的速度从点A出发,沿AD→DC的路径运动,到点C停止,过点P 作PQ⊥BD,PQ 与边AD(或边CD)交于点Q,△ABQ的面积y(cm2)与点P 的运动时间x(秒)的函数图象大致是( )

A. B.
B. C.
C.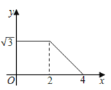 D.
D.
【答案】C
【解析】
由题意根据动点P的运动过程分两种情况说明:①PQ与边CD交于点Q时,过点D作DE⊥AB于点E,根据在边长为2一个内角为60°的菱形ABCD中,即可求当0≤x≤2时,y=![]() ;②当PQ与边AD交于点Q时,过点Q作QE⊥AB于点E,即可求当2<x≤4时,y=-
;②当PQ与边AD交于点Q时,过点Q作QE⊥AB于点E,即可求当2<x≤4时,y=-![]() x+4
x+4![]() ,进而可判断,△ABQ的面积y(cm2)与点P的运动时间x(秒)的函数图象.
,进而可判断,△ABQ的面积y(cm2)与点P的运动时间x(秒)的函数图象.
解:①PQ与边CD交于点Q时,
如图,过点D作DE⊥AB于点E,
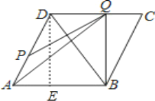
∴∠DEA=90°,
在边长为2一个内角为60°的菱形ABCD中,
AD=DC=2,∠DAB=60°,
∴AE=1,![]() ,
,
∴![]() ,
,
即当0≤x≤2时,![]() .
.
该函数图象是平行于x轴的一段线段;
②当PQ与边AD交于点Q时,如图,过点Q作QE⊥AB于点E,
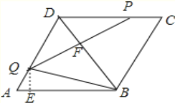
∴∠QEA=90°,
∵PQ⊥BD,
∴∠DFP=∠DFQ=90°,
∵四边形ABCD是菱形,
∴BD平分∠ADC,
∴∠CDB=∠ADB,
DF=DF,
∴△DFP≌△DFQ(ASA),
∴DP=DQ,
∵AD=DC=2,
∴AQ=PC=4-x,
∴在Rt△AQE中,∠QAE=60°,
∴![]() ,
,
∴![]()
即当2<x≤4时,![]() ,
,
该函数图象是y随x的增大而减小的一段线段.
所以△ABQ的面积y(cm2)与点P的运动时间x(秒)的函数图象大致是选项C.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,把一张直角三角形卡片ABC放在每格宽度为12mm的横格纸中,三个顶点恰好都落在横格线上,已知∠BAC=90°,∠α=36°,求直角三角形卡片ABC的面积(精确到1mm).(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点(0,-3).
的图象经过点(0,-3).
(1)求这个二次函数的函数解析式;
(2)当x取何值时,函数y的值随着x的增大而增大;
(3)当x取何值时,函数的值为0.
查看答案和解析>>
科目:初中数学 来源: 题型:
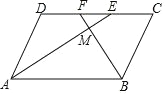
【题目】如图,在 ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.
(1)求证:AE⊥BF;
(2)判断线段 DF 与 CE 的大小关系,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个涵洞成抛物线形,它的截面如图,现测得:当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m,离开水面1.5 m处是涵洞宽ED.
(1)求抛物线的解析式;
(2)求ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2-2amx+am2+2m+4的顶点P在一条定直线l上.
(1)直接写出直线l的解析式;
(2)若存在唯一的实数m,使抛物线经过原点.
①求此时的a和m的值;
②抛物线的对称轴与x轴交于点A,B为抛物线上一动点,以OA、OB为边作□OACB,若点C在抛物线上,求B的坐标.
(3)抛物线与直线l的另一个交点Q,若a=1,直接写出△OPQ的面积的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级某班部分学生植树,若每人平均植树8棵,还剩7棵;若每人植树9棵,则有一名学生植树的棵树多于3棵而小于6棵.若设学生人数为x人,则植树棵树为(8x7)人,则下面给出的不等式(组)中,能准确求出学生人数与种植树木数量的是( )
A.8x769(x1)B.8x739(x1)
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AB=8,AD⊥BC,点E为线段AD上的动点,连接CE,以CE为边作等边△CEF,连接DF,则线段DF的最小值为( )

A.![]() B.4C.2D.无法确定
B.4C.2D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点。

(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法)。
①作∠DAC的平分线AM。②连接BE并延长交AM于点F。
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com