
【题目】如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF.△ABC旋转后能与△FBE重合,请回答:
(1)旋转中心是点____,
(2)旋转了____度,
(3) AC与EF的关系为_________.

【答案】 B 90 AC=EF,AC⊥EF
【解析】试题分析:(1)由条件易得BC和BE,BA和BF为对应边,而△ABC旋转后能与△FBE重合,于是可判断旋转中心为点B;
(2)根据旋转的性质得∠ABF等于旋转角,从而得到旋转角度;
(3)根据旋转的性质即可判断AC=EF,AC⊥EF.
试题解析:解:(1)∵BC=BE,BA=BF,∴BC和BE,BA和BF为对应边,∵△ABC旋转后能与△FBE重合,∴旋转中心为点B;
(2)∵∠ABC=90°,而△ABC旋转后能与△FBE重合,∴∠ABF等于旋转角,∴旋转了90度;
(3)AC=EF,AC⊥EF.理由如下:
∵△ABC绕点B顺时针旋转90°后能与△FBE重合,∴EF=AC,EF与AC成90°的角,即AC⊥EF.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】某校九年级有24个班,共1 000名学生,他们参加了一次数学测试.学校统计了所有学生的成绩,得到下列统计图.

(1)求该校九年级学生本次数学测试成绩的平均数;
(2)下列关于本次数学测试说法正确的是( )
A.九年级学生成绩的众数与平均数相等
B.九年级学生成绩的中位数与平均数相等
C.随机抽取一个班,该班学生成绩的平均数等于九年级学生成绩的平均数
D.随机抽取300名学生,可以用他们成绩的平均数估计九年级学生成绩的平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过 1 千克的,按每千克 22 元收费;超过 1 千克,超过的部分按每千克 15元收费.乙公司表示:按每千克 16 元收费,另加包装费 3 元.设小明快递物品x 千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用 y(元)与 x(千克)之间的函数关系式;
(2)当 ![]() 为何值时小明选择乙快递公司更省钱?
为何值时小明选择乙快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在对Rt△OAB依次进行位似、轴对称和平移变换后得到△O′A′B′.
(1)在坐标纸上画出这几次变换相应的图形;
(2)设P(x,y)为△OAB边上任一点,依次写出这几次变换后点P对应点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张直角三角形卡片ABC放在每格宽度为12mm的横格纸中,三个顶点恰好都落在横格线上,已知∠BAC=90°,∠α=36°,求直角三角形卡片ABC的面积(精确到1mm).(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2013的坐标为

A. (2,1006)B. (1008,0)C. ( -1006,0)D. (1,-1007)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贺岁片《流浪地球》被称为开启了中国科幻片的大门,2019也被称为中国科幻片的元年.某电影院为了全面了解观众对《流浪地球》的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).根据以上信息,解答下列问题:
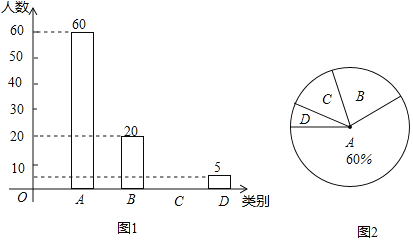
(1)本次接受调查的观众共有 人;
(2)扇形统计图中,扇形C的圆心角度数是 .
(3)请补全条形统计图;
(4)春节期间,该电影院来观看《流浪地球》的观众约3000人,请估计观众中对该电影满意(A、B、C类视为满意)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作ECFG.
(1)如图1,证明ECFG为菱形;
(2)如图2,若∠ABC=120°,连接BG、CG,并求出∠BDG的度数:
(3)如图3,若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2-2amx+am2+2m+4的顶点P在一条定直线l上.
(1)直接写出直线l的解析式;
(2)若存在唯一的实数m,使抛物线经过原点.
①求此时的a和m的值;
②抛物线的对称轴与x轴交于点A,B为抛物线上一动点,以OA、OB为边作□OACB,若点C在抛物线上,求B的坐标.
(3)抛物线与直线l的另一个交点Q,若a=1,直接写出△OPQ的面积的值或取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com