
【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE ,设∠BAD=α,∠CDE=β.
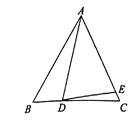
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°, 那么α=_______,β=_______.
②求α、β之间的关系式.
(2)是否存在不同于以上②中的α、β之间的关系式?若存在,求出这个关系式,若不存在,请说明理由.
【答案】(1)①20,10;②α=2β;(2)α=2β-180°.
【解析】
试题分析:(1)①在△ADE中,由AD=AE,∠ADE=70°,不难求出∠AED和∠DAE;由AB=AC,∠ABC=60°,可得∠BAC=∠C=∠ABC=60°,则α=∠BAC-∠DAE,再根据三角形外角的性质可得β=∠AED-∠C;②求解时可借助设未知数的方法,然后再把未知数消去的方法,可设∠ABC=x,∠ADE=y;(2)有很多种不同的情况,做法与(1)中的②类似,可求这种情况:点E在CA延长线上,点D在线段BC上.
试题解析:(1)①∵AD=AE,∴∠AED=∠ADE=70°,∠DAE=40°,又∵AB=AC,∠ABC=60°,∴∠BAC=∠C=∠ABC=60°,∴α=∠BAC-∠DAE=60°-40°=20°,β=∠AED-∠C=70°-60°=10°;
②设∠ABC=x,∠ADE=y,则∠ACB=x,∠AED=y,在△DEC中,y=β+x,在△ABD中,α+x=y+β,∴α=2β.
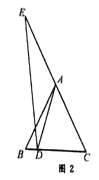
(2)如图2,点E在CA延长线上,点D在线段BC上,设∠ABC=x,∠ADE=y,则∠ACB=x,∠AED=y,在△ABD中,x+α=β-y,在△DEC中,x+y+β=180°,∴α=2β-180°.
注:求出其它关系式,相应给分,如点E在CA的延长线上,点D在CB的延长线上,可得α=180°-2β.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.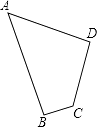
(1)判断∠D是否是直角,并说明理由.
(2)求四边形草坪ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示,△ABC的顶点均在格点上,其中每个小正方形的边长为1个单位长度,将△ABC绕原点O旋转180°得△A1B1C1 . 
(1)在图中画出△A1B1C1;
(2)写出点A1的坐标;
(3)求出点C所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】能判定四边形ABCD为平行四边形的题设是( )。
A. AB∥CD,AD=BC B. AB=CD,AD=BC
C. ∠A=∠B,∠C=∠D D. AB=AD,CB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠A=90°,DE∥BC,F,G,H,I分别是DE,BE,BC,CD的中点,连接FG,GH,HI,IF,FH,GI.对于下列结论:①∠GFI=90°;②GH=GI;③GI= ![]() (BC﹣DE);④四边形FGHI是正方形.其中正确的是(请写出所有正确结论的序号).
(BC﹣DE);④四边形FGHI是正方形.其中正确的是(请写出所有正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com