【题目】我市某储运部紧急调拨一批物资，调进物资共用4小时，调进物资2小时后开始调出物资（调进物资与调出物资的速度均保持不变）.储运部库存物资
（吨）与时间
（小时）之间的函数关系如图所示，这批物资从开始调进到全部调出需要的时间是（ ）
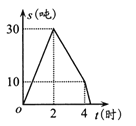
A. 4小时B. 4.3小时C. 4.4小时D. 5小时
科目：初中数学 来源： 题型：
【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系．如图，在平面上取定一点O称为极点；从点O出发引一条射线Ox称为极轴；线段OP的长度称为极径．点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度（规定逆时针方向转动角度为正）来确定，即P（3，60°）或P（3，﹣300°）或P（3，420°）等，则点P关于点O成中心对称的点Q的极坐标表示不正确的是（ ）
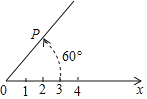
A. Q（3，240°） B. Q（3，﹣120°） C. Q（3，600°） D. Q（3，﹣500°）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线y＝﹣2x+1与y轴交于点A，与反比例函数y＝
（k为常数）的图象有一个交点B的纵坐标是5．
（Ⅰ）求反比例函数的解析式，并说明其图象所在的象限；
（Ⅱ）当2＜x＜5时，求反比例函数的函数值y的取值范围；
（Ⅲ）求△AOB的面积S．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有这样一个题目：
按照给定的计算程序，确定使代数式n（n+2）大于2000的n的最小正整数值．想一想，怎样迅速找到这个n值，请与同学们交流你的体会．
小亮尝试计算了几组n和n（n+2）的对应值如下表：
n | 50 | 40 | |
n（n+2） | 2600 | 1680 |
（1）请你继续小亮的尝试，再算几组填在上表中（几组随意，自己画格），并写出满足题目要求的n的值；
（2）结合上述过程，对于“怎样迅速找到n值”这个问题，说说你的想法．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
经过正方形网格中的格点
、
、
、
，请你仅用网格中的格点及无刻度的直尺分别在图1、图2、图3中画出一个满足下列两个条件的
：
（1）顶点
在上且不与点、、、重合；
（2）在图1、图2、图3中的正切值分别为1、
、2.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
是
（
）的函数，表1中给出了几组与的对应值：
表1：
| … |
| 1 |
| 2 |
| 3 | … |
| … | 6 | 3 | 2 |
|
| 1 | … |
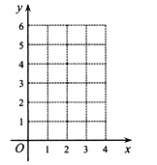
（1）以表中各对对应值为坐标，在图1的直角坐标系中描出各点，用光滑曲线顺次连接.由图像知，它是我们已经学过的哪类函数？求出函数解析式，并直接写出
的值；
（2）如果一次函数图像与（1）中图像交于
和
两点，在第一、四象限内当在什么范围时，一次函数的值小于（1）中函数的值？请直接写出答案.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校九年级为了解学生课堂发言情况，随机抽取该年级部分学生，对他们某天在课堂上发言的次数进行了统计，其结果如表，并绘制了如图所示的两幅不完整的统计图，已知B、E两组发言人数的比为5：2，请结合图中相关数据回答下列问题：
（1）则样本容量是 ，并补全直方图；
（2）该年级共有学生500人，请估计全年级在这天里发言次数不少于12的次数；
（3）已知A组发言的学生中恰有1位女生，E组发言的学生中有2位男生，现从A组与E组中分别抽一位学生写报告，请用列表法或画树状图的方法，求所抽的两位学生恰好是一男一女的概率．
发言次数n | |
A | 0≤n＜3 |
B | 3≤n＜6 |
C | 6≤n＜9 |
D | 9≤n＜12 |
E | 12≤n＜15 |
F | 15≤n＜18 |
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知顶点为P的抛物线C1的解析式为y=a(x-3)2(a≠0),且经过点(0,1).
(1)求a的值及抛物线C1的解析式;
(2)如图,将抛物线C1向下平移h(h>0)个单位得到抛物线C2,过点K(0,m2)(m>0)作直线l平行于x轴,与两抛物线从左到右分别相交于A,B,C,D四点,且A,C两点关于y轴对称.
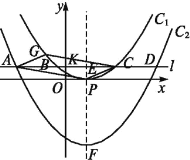
①点G在抛物线C1上,当m为何值时,四边形APCG为平行四边形?
②若抛物线C1的对称轴与直线l交于点E,与抛物线C2交于点F.试探究:在K点运动过程中,
的值是否改变?若会,请说明理由;若不会,请求出这个值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】大熊山某农家乐为了抓住“五一”小长假的商机，决定购进A、B两种纪念品。若购进A种纪念品4件，B种纪念品3件，需要550元；若购进A种纪念品8件，B种纪念品5件，需要1050元。
（1）求购进A、B两种纪念品每件各需多少元。
（2）若该农家乐决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于7500元，但不超过7650元，那么该农家乐共有几种进货方案。
（3）若销售每件A种纪念品可获利润30元，每件B种纪念品可获利润20元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少元。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
