Question

【题目】【阅读发现】如图①，在正方形ABCD的外侧，作两个等边三角形ABE和ADF，连结ED与FC交于点M，则图中△ADE≌△DFC，可知ED=FC，求得∠DMC= ．

【拓展应用】如图②，在矩形ABCD（AB＞BC）的外侧，作两个等边三角形ABE和ADF，连结ED与FC交于点M．

（1）求证：ED=FC．

（2）若∠ADE=20°，求∠DMC的度数．

Answer 1

【答案】90°；（1）证明见解析（2）100°

【解析】

试题分析：阅读发现：只要证明∠DFC=∠DCF=∠ADE=∠AED=15°，即可证明．

拓展应用：（1）欲证明ED=FC，只要证明△ADE≌△DFC即可．

（2）根据∠DMC=∠FDM+∠DFC=∠FDA+∠ADE+∠DFC即可计算．

试题解析：如图①中，∵四边形ABCD是正方形，

∴AD=AB=CD，∠ADC=90°，

∵△ADE≌△DFC，

∴DF=CD=AE=AD，

∵∠FDC=60°+90°=150°，

∴∠DFC=∠DCF=∠ADE=∠AED=15°，

∴∠FDE=60°+15°=75°，

∴∠MFD+∠FDM=90°，

∴∠FMD=90°，

故答案为90°

（1）∵△ABE为等边三角形，

∴∠EAB=60°，EA=AB．

∵△ADF为等边三角形，

∴∠FDA=60°，AD=FD．

∵四边形ABCD为矩形，

∴∠BAD=∠ADC=90°，DC=AB．

∴EA=DC．

∵∠EAD=∠EAB+∠BAD=150°，∠CDF=∠FDA+∠ADC=150°，

∴∠EAD=∠CDF．

在△EAD和△CDF中，

，

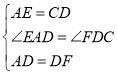∴△EAD≌△CDF．

∴ED=FC；

（2）∵△EAD≌△CDF，

∴∠ADE=∠DFC=20°，

∴∠DMC=∠FDM+∠DFC=∠FDA+∠ADE+∠DFC=60°+20°+20°=100°．