
【题目】如图,平面直角坐标系中,直线AB:![]() 交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
(1)求直线AB的解析式和点B的坐标;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.

【答案】(1) AB的解析式是y=-![]() x+1.点B(3,0).(2)
x+1.点B(3,0).(2)![]() n-1;(3) (3,4)或(5,2)或(3,2).
n-1;(3) (3,4)或(5,2)或(3,2).
【解析】
试题(1)把A的坐标代入直线AB的解析式,即可求得b的值,然后在解析式中,令y=0,求得x的值,即可求得B的坐标;
(2)过点A作AM⊥PD,垂足为M,求得AM的长,即可求得△BPD和△PAB的面积,二者的和即可求得;
(3)当S△ABP=2时,![]() n-1=2,解得n=2,则∠OBP=45°,然后分A、B、P分别是直角顶点求解.
n-1=2,解得n=2,则∠OBP=45°,然后分A、B、P分别是直角顶点求解.
试题解析:(1)∵y=-![]() x+b经过A(0,1),
x+b经过A(0,1),
∴b=1,
∴直线AB的解析式是y=-![]() x+1.
x+1.
当y=0时,0=-![]() x+1,解得x=3,
x+1,解得x=3,
∴点B(3,0).
(2)过点A作AM⊥PD,垂足为M,则有AM=1,
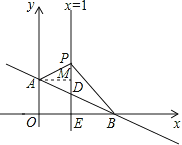
∵x=1时,y=-![]() x+1=
x+1=![]() ,P在点D的上方,
,P在点D的上方,
∴PD=n-![]() ,S△APD=
,S△APD=![]() PDAM=
PDAM=![]() ×1×(n-
×1×(n-![]() )=
)=![]() n-
n-![]()
由点B(3,0),可知点B到直线x=1的距离为2,即△BDP的边PD上的高长为2,
∴S△BPD=![]() PD×2=n-
PD×2=n-![]() ,
,
∴S△PAB=S△APD+S△BPD=![]() n-
n-![]() +n-
+n-![]() =
=![]() n-1;
n-1;
(3)当S△ABP=2时,![]() n-1=2,解得n=2,
n-1=2,解得n=2,
∴点P(1,2).
∵E(1,0),
∴PE=BE=2,
∴∠EPB=∠EBP=45°.
第1种情况,如图1,∠CPB=90°,BP=PC,过点C作CN⊥直线x=1于点N.
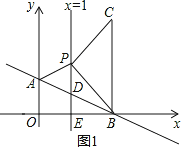
∵∠CPB=90°,∠EPB=45°,
∴∠NPC=∠EPB=45°.
又∵∠CNP=∠PEB=90°,BP=PC,
∴△CNP≌△BEP,
∴PN=NC=EB=PE=2,
∴NE=NP+PE=2+2=4,
∴C(3,4).
第2种情况,如图2∠PBC=90°,BP=BC,
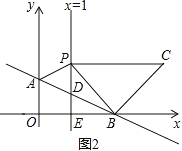
过点C作CF⊥x轴于点F.
∵∠PBC=90°,∠EBP=45°,
∴∠CBF=∠PBE=45°.
又∵∠CFB=∠PEB=90°,BC=BP,
∴△CBF≌△PBE.
∴BF=CF=PE=EB=2,
∴OF=OB+BF=3+2=5,
∴C(5,2).
第3种情况,如图3,∠PCB=90°,CP=EB,
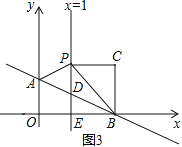
∴∠CPB=∠EBP=45°,
在△PCB和△PEB中,
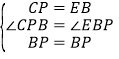
∴△PCB≌△PEB(SAS),
∴PC=CB=PE=EB=2,
∴C(3,2).
∴以PB为边在第一象限作等腰直角三角形BPC,点C的坐标是(3,4)或(5,2)或(3,2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
A.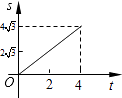
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点,作BM⊥AE于点M,作KN⊥AE于点N,连结MO、NO,以下四个结论:①△OMN是等腰三角形;②tan∠OMN= ![]() ;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )
;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别是(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的图形的面积为( )
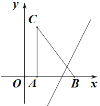
A. 4 B. 8 C. 16 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则 ![]() 的值为 .
的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
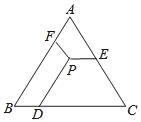
A. 18B. 9![]()
C. 6D. 条件不够,不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似(不包括全等)?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
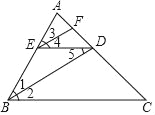
【题目】如图,BD是∠ABC的平分线,ED∥BC,∠4=∠5,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线(已知)
∴∠1=∠2(角平分线定义)
∵ED∥BC(已知)
∴∠5=∠2( )
∴∠1=∠5(等量代换)
∵∠4=∠5(已知)
∴EF∥ ( )
∴∠3=∠1( )
∴∠3=∠4(等量代换)
∴EF是∠AED的平分线(角平分线定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底角为72°,腰AB的垂直平分线交另一腰AC于点E,垂足为D,连接BE,则下列结论错误的是( )
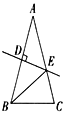
A. ∠EBC为36° B. BC = AE
C. 图中有2个等腰三角形 D. DE平分∠AEB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com