
【题目】读图并回答下列问题:
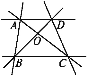
(1)过点A的直线有哪几条?
(2)以O为端点的射线有哪几条?
(3)写出图中所有的线段.
(4)∠ABC是哪两个角的和?
(5)比较线段AB,OB的长短.
【答案】(1)有三条:直线AB、直线AC、直线AD;(2)有四条:射线OA、射线OB、射线OC、射线OD;(3)线段AB,BC,CD,AD,OA,OC,OB,OD,AC,BD;(4)∠ABO与∠CBO;(5) AB>OB.
【解析】
(1)图中过点A的直线有三条;
(2)根据数射线的方法数出即可;
(3)根据数线段的方法数出即可;
(4)由图即可得出;
(5)用度量法或圆规即可比较.
(1)过点A的直线有三条:直线AB、直线AC、直线AD;
(2)以O为端点的射线有四条:射线OA、射线OB、射线OC、射线OD;
(3)图中的线段分别为线段AB,BC,CD,AD,OA,OC,OB,OD,AC,BD;
(4)∠ABO与∠CBO;
(5)利用刻度尺或圆规可得AB>OB.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知CA⊥BA
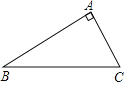
(1)画图:①延长BA到D,使AD=BA,连接CD;
②过点A画AE∥BC,AE与CD相交于点E;
③过点B画BF⊥CD,交DC的延长线于点F.
思考:图中有______条线段,它们的长度表示点到直线的距离;
(2)度量:
①你度量的哪些量?______;
②通过度量你发现:______.(写一条发现即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别写有数字-1,1,2的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片随机抽一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
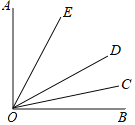
【题目】如图,已知∠AOB内部有三条射线,OE平分∠AOD,OC平分∠BOD.
(1)若∠AOB=90°,求∠EOC的度数;
(2)若∠AOB=α,求∠EOC的度数;
(3)如果将题中“平分”的条件改为∠EOA=![]() ∠AOD,∠DOC=
∠AOD,∠DOC=![]() ∠DOB,∠AOD=50°,且∠AOB=90°,求∠EOC的度数.
∠DOB,∠AOD=50°,且∠AOB=90°,求∠EOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时),图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图像线段AB表示甲出发不足2小时因故停车检修),请根据图像所提供的信息,解决如下问题:
(1)求乙车所行路程y与时间x的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇?(写出解题过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
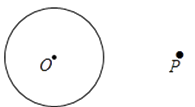
小敏的作法如下:
如图,
①链接op,做线段op的垂直平分线MN,交OP于点C
②以点C为圆心,CO的长为半径作圆,交⊙O于A、B两点
③作直线PA、PB所以直线PA,PB就是所求的切线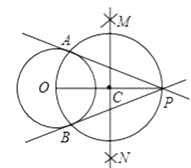
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界读书日,新华书店矩形购书优惠活动:①一次性购书不超过100元,不享受打折优惠;②一次性购书超过100元但不超过200元一律八折;③一次性购书200元以上一律打六折.小丽在这次活动中,两次购书总共付款190.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F. 
(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)写出求图中阴影部分的面积的思路.(不求计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
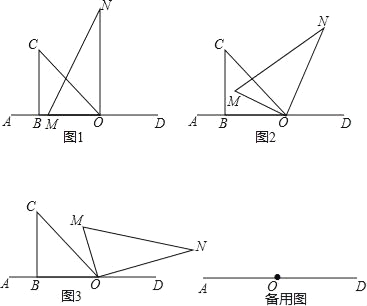
【题目】将一副直角三角板按如图1 摆放在直线AD 上(直角三角板OBC 和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC 不动,将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒.
(1)如图2,当t= 秒时,OM 平分∠AOC,此时∠NOC﹣∠AOM= ;
(2)继续旋转三角板MON,如图3,使得OM、ON 同时在直线OC 的右侧,猜想∠NOC与∠AOM 有怎样的数量关系?并说明理由(数量关系中不能含t);
(3)直线AD 的位置不变,若在三角板MON 开始顺时针旋转的同时,另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转,当OM 旋转至射线OD 上时,两个三角板同时停止运动.
①当t= 秒时,∠MOC=15°;
②请直接写出在旋转过程中,∠NOC 与∠AOM 的数量关系(数量关系中不能含t).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com