
【题目】世界读书日,新华书店矩形购书优惠活动:①一次性购书不超过100元,不享受打折优惠;②一次性购书超过100元但不超过200元一律八折;③一次性购书200元以上一律打六折.小丽在这次活动中,两次购书总共付款190.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是_____元.
【答案】224或272.
【解析】
设小丽第一次购书的原价为x元,则第二次购书的原价为3x元,分x≤![]() 、
、![]() <x≤
<x≤![]() 、
、![]() <x≤100及x>100四种情况,找出关于x的一元一次方程,解之即可得出结论.
<x≤100及x>100四种情况,找出关于x的一元一次方程,解之即可得出结论.
设小丽第一次购书的原价为x元,则第二次购书的原价为3x元,根据题意,分四种情况讨论:
①当3x≤100,即x≤![]() 时,x+3x=190.4,解得:x=47.6(舍去);
时,x+3x=190.4,解得:x=47.6(舍去);
②当100<3x≤200,即![]() <x≤
<x≤![]() 时,x+0.8×3x=190.4,解得:x=56,∴x+3x=224;
时,x+0.8×3x=190.4,解得:x=56,∴x+3x=224;
③当3x>200且x≤100,即![]() <x≤100时,x+0.6×3x=190.4,解得:x=68,∴x+3x=272;
<x≤100时,x+0.6×3x=190.4,解得:x=68,∴x+3x=272;
④当x>100时,0.8x+0.6×3x=190.4,解得:x≈73.23(舍去).
综上所述:小丽这两次购书原价的总和是224元或272元.
故答案为:224或272.


科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.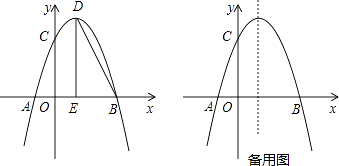
(Ⅰ)求抛物线的解析式及点D的坐标;
(Ⅱ)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(Ⅲ)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在”元旦“期间,罗山县尚文学校七一班的小明、小亮等同学随家长一同到信阳波尔登森林公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
(1)小明他们一共去了几个成人,几个学生?
(2)小明用所学的数字知识很快算出了哪种方式更省钱,你知道吗?请写出你的推算过程.
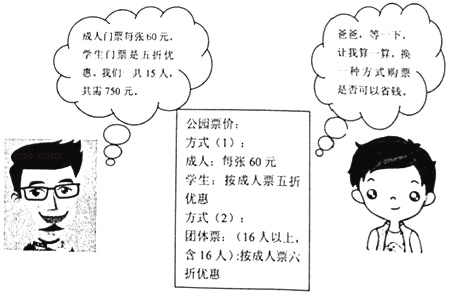
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc﹣ad.
例如:(1,2)★(3,4)=2×3﹣1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,﹣3)★(3,﹣2)= ;
(2)若有理数对(﹣3,2x﹣1)★(1,x+1)=7,则x= ;
(3)当满足等式(﹣3,2x﹣1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.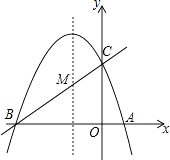
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N.求证:△ABN≌△CDM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图(1)中,对任意相邻的上下或左右两格中的数字同时加1或减2,这算作一次操作,经过若干次操作后,图(1)能变为图(2),则图(2)中A格内的数是_____
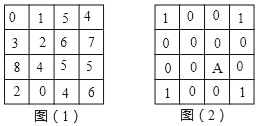
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com