
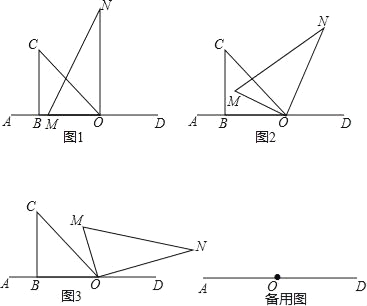
【题目】将一副直角三角板按如图1 摆放在直线AD 上(直角三角板OBC 和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC 不动,将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒.
(1)如图2,当t= 秒时,OM 平分∠AOC,此时∠NOC﹣∠AOM= ;
(2)继续旋转三角板MON,如图3,使得OM、ON 同时在直线OC 的右侧,猜想∠NOC与∠AOM 有怎样的数量关系?并说明理由(数量关系中不能含t);
(3)直线AD 的位置不变,若在三角板MON 开始顺时针旋转的同时,另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转,当OM 旋转至射线OD 上时,两个三角板同时停止运动.
①当t= 秒时,∠MOC=15°;
②请直接写出在旋转过程中,∠NOC 与∠AOM 的数量关系(数量关系中不能含t).
【答案】(1) t=2.8125,45;(2)∠NOC﹣∠AOM=45°;(3)①5或10;②![]() ∠NOC﹣
∠NOC﹣![]() ∠AOM=15°.
∠AOM=15°.
【解析】
(1)根据角平分线的定义得到∠AOM=![]() ∠AOC=22.5°,于是得到t=2.8125,由于∠MON=90°,∠MOC=22.5°,即可得到∠NOC﹣∠AOM=∠MON﹣∠MOC﹣∠AOM=45°;
∠AOC=22.5°,于是得到t=2.8125,由于∠MON=90°,∠MOC=22.5°,即可得到∠NOC﹣∠AOM=∠MON﹣∠MOC﹣∠AOM=45°;
(2)根据题意得∠AON=90°+8t,求得∠NOC=90°+8t﹣45°=45°+8t,即可得到结论;
(3)①根据题意得∠AOB=2t,∠AOM=8t,求得∠AOC=45°+2t,列方程即可得到结论;
②根据角的和差即可得到结论.
(1)∵∠AOC=45°,OM平分∠AOC,∴∠AOM=![]() ∠AOC=22.5°,∴t=2.8125.
∠AOC=22.5°,∴t=2.8125.
∵∠MON=90°,∠MOC=22.5°,∴∠NOC﹣∠AOM=∠MON﹣∠MOC﹣∠AOM=45°;
(2)∠NOC﹣∠AOM=45°.
∵∠AON=90°+8t,∴∠NOC=90°+8t﹣45°=45°+8t.
∵∠AOM=8t,∴∠NOC﹣∠AOM=45°;
(3)①∵∠AOB=2t,∠AOM=8t,∴∠AOC=45°+2t,∴45°+2t﹣8t=15°或8t﹣45°﹣2t=15°.
解得:t=5或10.
②![]() ∠NOC﹣
∠NOC﹣![]() ∠AOM=15°.
∠AOM=15°.
∵∠AOB=2t,∠AOM=8t,∠MON=90°,∠BOC=45°.
∵∠AON=90°+∠AOM=90°+8t,∠AOC=∠AOB+∠BOC=45°+2t,∴∠NOC=∠AON﹣∠AOC=90°+8t﹣45°﹣2t=45°+6t,∴![]() ∠NOC﹣
∠NOC﹣![]() ∠AOM=15°.
∠AOM=15°.


科目:初中数学 来源: 题型:
【题目】读图并回答下列问题:
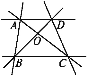
(1)过点A的直线有哪几条?
(2)以O为端点的射线有哪几条?
(3)写出图中所有的线段.
(4)∠ABC是哪两个角的和?
(5)比较线段AB,OB的长短.
查看答案和解析>>
科目:初中数学 来源: 题型:
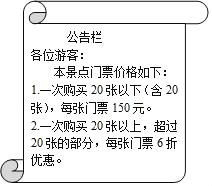
【题目】2018年国庆期间,一旅游团到安徽境内某旅游景点,看到售票处旁边的公告栏如图所示,请根据公告栏内容解答下列问题:(答案直接写在横线上)
(1)若旅游团人数为18人,门票费用是 元;若旅游团人数为22人,门票费用为 _______元.
(2)设旅游团人数为x人,试用含量x的代数式表示该旅游团门票费用y元.
(解)y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条直线相交,只有1个交点,三条直线相交,最多有3个交点,四条直线相交,最多有6个交点,10条直线相交,最多有( )个交点.
A. 45 B. 42 C. 40 D. 36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=90°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1 , AA2 , AA3…,依此作法,则∠AAnAn+1等于度.(用含n的代数式表示,n为正整数) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣6,0),B(2,0),C(0,﹣6).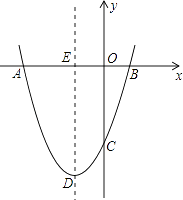
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有( ) 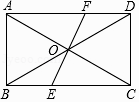
A.5对
B.6对
C.8对
D.10对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条长为60cm的卷尺铺平后沿着图中箭头的方向折叠,使得卷尺自身的一部分重合,然后在重合部分沿与卷尺的边垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度比为1:2:3,则折痕对应的刻度可能的值有 ________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
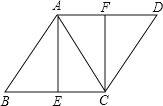
【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
(1)求证:四边形AECF是矩形;
(2)若AB=6,求菱形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com