
【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
(1)求证:四边形AECF是矩形;
(2)若AB=6,求菱形的面积.
【答案】(1)证明见解析;(2)24![]()
【解析】试题(1)首先证明△ABC是等边三角形,进而得出∠AEC=90°,四边形AECF是平行四边形,即可得出答案;
(2)利用勾股定理得出AE的长,进而求出菱形的面积.
试题解析:(1)∵四边形ABCD是菱形,
∴AB=BC,
又∵AB=AC,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC,
∴∠AEC=90°,
∵E、F分别是BC、AD的中点,
∴AF=![]() AD,EC=
AD,EC=![]() BC,
BC,
∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∴AF∥EC且AF=EC,
∴四边形AECF是平行四边形,
又∵∠AEC=90°,
∴四边形AECF是矩形;
(2)在Rt△ABE中,AE=![]() ,
,
所以,S菱形ABCD=6×3![]() =18
=18![]() .
.


科目:初中数学 来源: 题型:
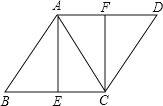
【题目】将一副直角三角板按如图1 摆放在直线AD 上(直角三角板OBC 和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC 不动,将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒.
(1)如图2,当t= 秒时,OM 平分∠AOC,此时∠NOC﹣∠AOM= ;
(2)继续旋转三角板MON,如图3,使得OM、ON 同时在直线OC 的右侧,猜想∠NOC与∠AOM 有怎样的数量关系?并说明理由(数量关系中不能含t);
(3)直线AD 的位置不变,若在三角板MON 开始顺时针旋转的同时,另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转,当OM 旋转至射线OD 上时,两个三角板同时停止运动.
①当t= 秒时,∠MOC=15°;
②请直接写出在旋转过程中,∠NOC 与∠AOM 的数量关系(数量关系中不能含t).
查看答案和解析>>
科目:初中数学 来源: 题型:
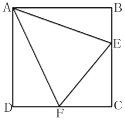
【题目】如图,E与F分别在正方形ABCD边BC与CD上,∠EAF=45°.
(1)以A为旋转中心,将△ABE按顺时针方向旋转90°,画出旋转后得到的图形.
(2)已知BE=2cm,DF=3cm,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“低碳生活”的号召,李明决定每天骑自行车上学,有一天李明骑了1000米后,自行车发生了故障,修车耽误了5分钟,车修好后李明继续骑行,用了8分钟骑行了剩余的800米,到达学校(假设在骑车过程中匀速行驶).若设他从家开始去学校的时间为t(分钟),离家的路程为y(千米),则y与t(15<t≤23)的函数关系为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天数学课上,老师讲了整式的加减.放学后,小明回到家拿出课堂笔记,认真地复习老师课堂上讲的内容,他突然发现一道题:
(﹣x2+3yx﹣![]() y2)﹣(﹣
y2)﹣(﹣![]() x2+■xy﹣
x2+■xy﹣![]() y2)=﹣
y2)=﹣![]() x2﹣xy+■y2,其中两处横线地方的数字被钢笔水弄污了,那么这两处地方的数字之积应是__.
x2﹣xy+■y2,其中两处横线地方的数字被钢笔水弄污了,那么这两处地方的数字之积应是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂质检部门对一批水果罐头的质量进行检查,从中随意抽查了10个,净含量如下(单位:g):339,343,341,347,345,341,340,344,329,341.
(1)这个问题中,总体、个体、样本各是什么?
(2)试估计出这批水果罐头的平均质量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将5张都是10元的纸币随机装入10个完全相同的信封中,设计以下几种抽奖游戏:
(1)游戏A:设计一个游戏,使任意抽取一个信封时,能抽到纸币的概率为![]() ;
;
(2)游戏B:设计一个游戏,使任意抽取一个信封时,能抽到纸币的概率为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB,AC的垂直平分线分别交BC于D,E两点,垂足分别是M,N.
(1)若△ADE的周长是10,求BC的长;
(2)若∠BAC=100°,求∠DAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
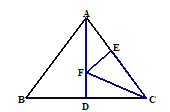
【题目】如图,△ABC中,AB=AC=5,BC=6,AD是BC边上的中线且AD=4,![]() 是AD上的动点,
是AD上的动点,![]() 是AC边上的动点,则
是AC边上的动点,则![]() 的最小值是( ).
的最小值是( ).
A. 6 B. 4 C. ![]() D. 不存在最小值
D. 不存在最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com