练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在矩形ABCD中，点O为对角线AC、BD的交点，点E为BC上一点，连接EO，并延长交AD于点F，则图中全等三角形共有（ ）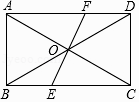
    A.5对
    B.6对
    C.8对
    D.10对

    【答案】D
    【解析】解：∵四边形ABCD为矩形，其矩形的对角线相等且相互平分， ∴AB=CD，AD=BC，AO=CO，BO=DO，EO=FO，∠DAO=∠BCO，
    又∠AOB=∠COD，∠AOD=∠COB，∠AOE=∠COF，
    易证△ABC≌△DCB，△ABC≌△CDA，△ABC≌△BAD，△BCD≌△ADC，△BCD≌△DAB，△ADC≌△DAB，△AOF≌△COE，△DOF≌△BOE，△DOC≌△AOB，△AOD≌△BOC故图中的全等三角形共有10对．
    故选D．
    根据已知及全等三角形的判定方法进行分析，从而得到答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】世界读书日，新华书店矩形购书优惠活动：①一次性购书不超过100元，不享受打折优惠；②一次性购书超过100元但不超过200元一律八折；③一次性购书200元以上一律打六折．小丽在这次活动中，两次购书总共付款190.4元，第二次购书原价是第一次购书原价的3倍，那么小丽这两次购书原价的总和是_____元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，各正方形的边长均为1，则四个阴影三角形中，一定相似的一对是（ ）
    A.①②
    B.①③
    C.②③
    D.②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

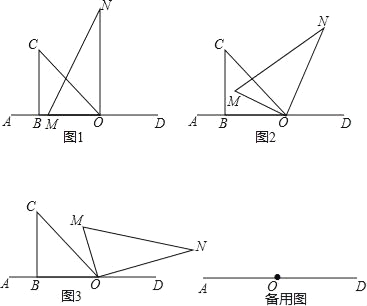
    【题目】将一副直角三角板按如图1 摆放在直线AD 上（直角三角板OBC 和直角三角板MON，∠OBC=90°，∠BOC=45°，∠MON=90°，∠MNO=30°），保持三角板OBC 不动，将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒．

    （1）如图2，当t=　 　秒时，OM 平分∠AOC，此时∠NOC﹣∠AOM= ；

    （2）继续旋转三角板MON，如图3，使得OM、ON 同时在直线OC 的右侧，猜想∠NOC与∠AOM 有怎样的数量关系？并说明理由（数量关系中不能含t）；

    （3）直线AD 的位置不变，若在三角板MON 开始顺时针旋转的同时，另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转，当OM 旋转至射线OD 上时，两个三角板同时停止运动．

    ①当t= 秒时，∠MOC=15°；

    ②请直接写出在旋转过程中，∠NOC 与∠AOM 的数量关系（数量关系中不能含t）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

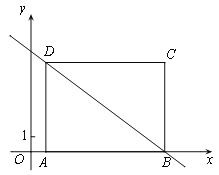
    【题目】如图，在平面直角坐标系xOy中，矩形ABCD的边AD=6，A（1，0）， B（9，0），直线y=kx+b经过B、D两点．

    （1）求直线y=kx+b的表达式；

    （2）将直线y=kx+b平移，当它与矩形没有公共点时，直接写出b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在读书月活动中，某校号召全体师生积极捐书，为了解所捐书籍的种类，图书管理员对部分书籍进行了抽样调查，根据调查数据绘制了如下不完整的统计图表．请你根据统计图表所提供的信息回答下面问题：

    某校师生捐书种类情况统计表

    种类

    频数

    百分比

    A．科普类

    12

    n

    B．文学类

    14

    35%

    C．艺术类

    m

    20%

    D．其它类

    6

    15%

    （1）统计表中的m= ，n= ；

    （2）补全条形统计图；

    （3）本次活动师生共捐书2000本，请估计有多少本科普类图书？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

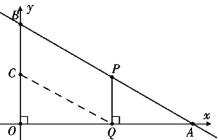
    【题目】已知如图：直线AB解析式为，其图像与坐标轴x,y轴分别相交于A、B两点，点P在线段AB上由A向B点以每秒2个单位运动，点C在线段OB上由O向B点以每秒1个单位运动（其中一点先到达终点则都停止运动），过点P与x轴垂直的直线交直线AO于点Q. 设运动的时间为t秒（t≥0）.

    （1）直接写出：A、B两点的坐标A( )，B( ).

    ∠BAO=______________度；

    （2）用含t的代数式分别表示：CB＝ ，PQ＝ ；

    （3）是否存在t的值，使四边形PBCQ为平行四边形？若存在，求出t的值；若不存在，说明理由；

    （4）（3分）是否存在t的值，使四边形PBCQ为菱形？若存在，求出t的值；若不存在，说明理由，

    并探究如何改变点C的速度（匀速运动），使四边形PBCQ在某一时刻为菱形，求点C的速度和时

    间t.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

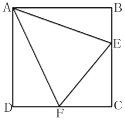
    【题目】如图，E与F分别在正方形ABCD边BC与CD上，∠EAF=45°.

    （1）以A为旋转中心，将△ABE按顺时针方向旋转90°，画出旋转后得到的图形.

    （2）已知BE=2cm，DF=3cm，求EF的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将5张都是10元的纸币随机装入10个完全相同的信封中，设计以下几种抽奖游戏：

    (1)游戏A：设计一个游戏，使任意抽取一个信封时，能抽到纸币的概率为；

    (2)游戏B：设计一个游戏，使任意抽取一个信封时，能抽到纸币的概率为.

    查看答案和解析>>

    同步练习册答案