
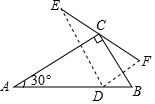
 如图,在Rt△ABC中,AC=4,∠A=30°,点D在斜边AB上,点D关于AC、BC的对称点为E、F,则EF的最小值是( )
如图,在Rt△ABC中,AC=4,∠A=30°,点D在斜边AB上,点D关于AC、BC的对称点为E、F,则EF的最小值是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 先连接CD,根据轴对称的性质,得出Rt△DEF中,CD=$\frac{1}{2}$EF,再根据垂线段最短,得出CD=$\frac{1}{2}$AC=2,最后根据直角三角形斜边上的中线性质,计算EF的最小值.
解答  解:连接CD,
解:连接CD,
∵点D关于AC、BC的对称点为E、F,
∴AC垂直平分DE,BC垂直平分DF,
∴CE=CD=CF,即C为EF的中点,
∵∠ACB=90°,
∴∠EDF=90°,
∴Rt△DEF中,CD=$\frac{1}{2}$EF,
∵点D在斜边AB上,
∴当CD⊥AB时,CD最短,
∵AC=4,∠A=30°,
∴当CD⊥AB时,CD=$\frac{1}{2}$AC=2,
此时,EF=2CD=2×2=4,
∴EF的最小值是4.
故选(C)
点评 本题主要考查了轴对称的性质、直角三角形的性质的综合应用,解决问题的关键是运用垂线段最短以及直角三角形斜边上的中线性质进行判断.


科目:初中数学 来源: 题型:选择题
| A. | x(x+1)=81 | B. | 1+x+x2=81 | C. | (1+x)2=81 | D. | 1+(1+x)2=81 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示的圆柱体中底面圆的半径是$\frac{2}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是$\sqrt{13}$.(结果保留根号)
如图所示的圆柱体中底面圆的半径是$\frac{2}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是$\sqrt{13}$.(结果保留根号)查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月月考数学试卷(解析版) 题型:单选题
如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB为( )
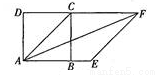
A. 22.5° B. 45° C. 30° D. 135°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com