
【题目】阅读下列材料:
对于多项式![]() ,如果我们把
,如果我们把![]() 代入此多项式,发现
代入此多项式,发现![]() 的值为0,这时可以确定多项式中有因式
的值为0,这时可以确定多项式中有因式![]() :同理,可以确定多项式中有另一个因式
:同理,可以确定多项式中有另一个因式![]() ,于是我们可以得到:
,于是我们可以得到:![]() .
.
又如:对于多项式![]() ,发现当
,发现当![]() 时,
时,![]() 的值为0,则多项式
的值为0,则多项式![]() 有一个因式
有一个因式![]() ,我们可以设
,我们可以设![]() ,解得
,解得![]() ,
,![]() ,于是我们可以得到:
,于是我们可以得到:![]() .
.
请你根据以上材料,解答以下问题:
(1)当![]() 时,多项式
时,多项式![]() 的值为0,所以多项式
的值为0,所以多项式![]() 有因式 ,从而因式分解
有因式 ,从而因式分解![]() .
.
(2)以上这种因式分解的方法叫试根法,常用来分解一些比较复杂的多项式.请你尝试用试根法分解多项式:①![]() ;②
;②![]() .
.
(3)小聪用试根法成功解决了以上多项式的因式分解,于是他猜想:
代数式![]() 有因式 , , ,
有因式 , , ,
所以分解因式![]() .
.
【答案】(1)![]() ;
;![]() ,
,![]() ;(2)①
;(2)①![]() ②
②![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)当x=1是,多项式![]() 的值为0,所以可设
的值为0,所以可设![]() ,然后求解得到m,n的值即可;
,然后求解得到m,n的值即可;
(2)①把x=﹣1代入![]() ,得到的值为0,则可设
,得到的值为0,则可设![]() ,然后根据题意求解m,n的值即可;
,然后根据题意求解m,n的值即可;
②同理①利用试根法进行求解即可;
(3)当x=2或y=2或x=y时都可得式子![]() =0,根据题意可得其有因式
=0,根据题意可得其有因式![]() ,然后将代数式
,然后将代数式![]() 去括号化简,将
去括号化简,将![]() 也去括号化简即可得到其关系.
也去括号化简即可得到其关系.
(1)当x=1是,多项式![]() =0,
=0,
则![]() ,
,
解得m=6,n=5,
∴![]() ;
;
(2)①当x=﹣1时,多项式![]() =0,
=0,
则![]() ,
,
解得m=2,n=3,
∴![]() ;
;
②当x=1或2时,多项式![]() =0,
=0,
则![]() ,
,
解得m=1,n=3,
∴![]() ;
;
(3)由题意可得当x=2或y=2或x=y时,多项式![]() =0,
=0,
则![]() 有因式
有因式![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】大润发超市在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,超市应将这种商品的售价定为多少?
(2)设每件商品的售价为x元,超市所获利润为y元.
①求y与x之间的函数关系式;
②物价局规定该商品的售价不能超过40元/件,超市为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
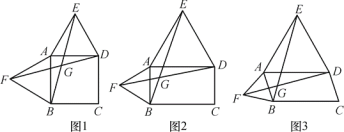
【题目】以四边形ABCD的边AB,AD为边分别向外侧作等边△ABF和等边△ADE,连接EB,FD,交点为G.
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2﹣4x+3与x轴交于A,B两点,其顶点为C.
(1)对于任意实数m,点M(m,﹣2)是否在该抛物线上?请说明理由;
(2)求证:△ABC是等腰直角三角形;
(3)若点D在x轴上,则在抛物线上是否存在点P,使得PD∥BC,且PD=BC?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知菱形![]() 的边长为12,
的边长为12,![]() , 点
, 点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的动点(不与端点重合),且
上的动点(不与端点重合),且![]() .
.
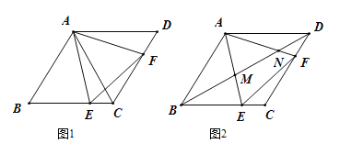
(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)点![]() 、
、![]() 在运动过程中,四边形
在运动过程中,四边形![]() 的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
(3)如图2,连接![]() 分别与边
分别与边![]() 、
、![]() 交于
交于![]() 、
、![]() ,当
,当![]() 时,求证:
时,求证:![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
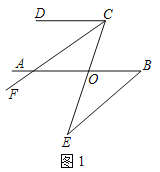
【题目】(1)如图1,AB∥CD,CF平分∠DCE,若∠DCF=30°,∠E=20°,求∠ABE的度数.
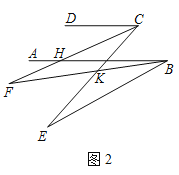
(2)如图2,已知AB∥CD,CF平分∠DCE,∠EBF=2∠ABF,若∠F的2倍与∠E的补角的和为190°,求∠ABE的度数.
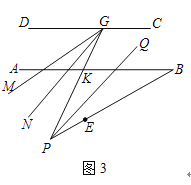
(3)如图3,若P是(2)中的射线BE上一点,G是CD上任一点,PQ∥GN,PQ平分∠BPG,GM平分∠DGP,若∠B=30°,求∠MGN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一根长22cm的铁丝:
(1)能否围成面积是30cm2的扇形?若能,求出扇形半径;若不能,请说明理由.
(2)能否围成面积是32cm2的扇形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
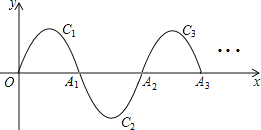
【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C17.
(1)写出点![]() 的坐标________
的坐标________
(2)若P(50,m)在第17段抛物线C17上,则m=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com