练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】二次函数y＝ax2+bx+c的部分对应值如表：

    利用该二次函数的图象判断，当函数值y＞0时，x的取值范围是（ ）

    A.0＜x＜8B.x＜0或x＞8C.﹣2＜x＜4D.x＜﹣2或x＞4

    【答案】C

    【解析】

    观察表格得出抛物线顶点坐标是(1，9)，对称轴为直线x=1，而当x=-2时，y=0，则抛物线与x轴的另一交点为(4，0)，由表格即可得出结论．

    由表中的数据知，抛物线顶点坐标是(1，9)，对称轴为直线x=1.当x＜1时，y的值随x的增大而增大，当x＞1时，y的值随x的增大而减小，则该抛物线开口方向向上，

    所以根据抛物线的对称性质知，点(﹣2，0)关于直线直线x=1对称的点的坐标是(4，0)．

    所以，当函数值y＞0时，x的取值范围是﹣2＜x＜4．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】对于长度为4的线段AB（图1），小若用尺规进行如下操作（图2）根据作图痕迹，有下列说法：①△ABC是等腰三角形；②△ABC是直角三角形；③△ABC是等边三角形；④弧AD的长度为，⑤△ABC是直角三角形的依据是直径所对的圆周角为直角，则其中正确的个数是（　　）

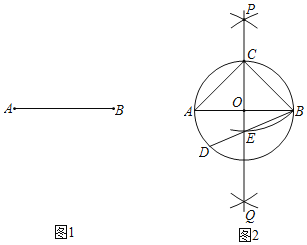
    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场要经营一种新上市的文具，进价为20元，试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件

    （1）写出商场销售这种文具，每天所得的销售利润（元）与销售单价（元）之间的函数关系式；

    （2）求销售单价为多少元时，该文具每天的销售利润最大；

    （3）商场的营销部结合上述情况，提出了A、B两种营销方案

    方案A：该文具的销售单价高于进价且不超过30元；

    方案B：每天销售量不少于10件，且每件文具的利润至少为25元

    请比较哪种方案的最大利润更高，并说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线的函数表达式为，它与轴、轴的交点分别为两点．

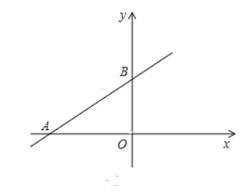
    （1）若的半径为2，说明直线与的位置关系；

    （2）若的半径为2，经过点且与轴相切于点，求圆心的坐标；

    （3）若的内切圆圆心是点，外接圆圆心是点，请直接写出的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一名大学生利用“互联网+”自主创业，销售一种产品，这种产品的成本价为24元/件，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于32元件，市场调查发现，该产品每天的销售最（件）与（元/件）之间的函数关系如图所示．

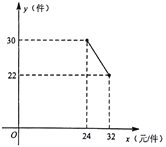
    （1）求与之间的函数关系式，并写出自变量的取值范围；

    （2）求每天的销售利润（元）与销售单价（元/件）之问的函数关系式并求出每天销售价为多少元时，每天的销售利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】超速行驶被称为“马路第一杀手”，为了让驾驶员自觉遵守交通规则，市公路检测中在一事故多发地段安装了一个测速仪器，如图所示，已知检测点A设在距离公路BC20米处，∠B＝45°，∠C＝30°，现测得一辆汽车从B处行驶到C处所用时间为2.7秒．

    （1）求B，C之间的距离（结果保留根号）；

    （2）如果此地限速为80km/h，那么这辆汽车是否超速？请说明理由．（参考数据：1.7，≈1.4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

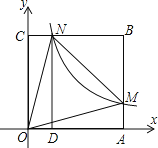
    【题目】如图，在直角坐标系中，正方形OABC的顶点O与原点重合，顶点A．C分别在x轴、y轴上，反比例函数的图象与正方形的两边AB、BC分别交于点M、N，ND⊥x轴，垂足为D，连接OM、ON、MN．

    下列结论：

    ①△OCN≌△OAM；

    ②ON=MN；

    ③四边形DAMN与△MON面积相等；

    ④若∠MON=45°，MN=2，则点C的坐标为．

    其中正确的个数是（ ）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，并完成相应的任务．

    古希腊的几何学家海伦在他的著作《度量论》一书中给出了利用三角形三边之长求面积的公式﹣﹣﹣﹣海伦公式S＝（其中a，b，c是三角形的三边长，，S为三角形的面积），并给出了证明

    例如：在△ABC中，a＝3，b＝4，c＝5，那么它的面积可以这样计算：

    ∵a＝3，b＝4，c＝5

    ∴＝6

    ∴S＝＝＝6

    事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．

    根据上述材料，解答下列问题：

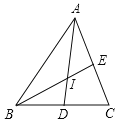
    如图，在△ABC中，BC＝7，AC＝8，AB＝9

    （1）用海伦公式求△ABC的面积；

    （2）如图，AD、BE为△ABC的两条角平分线，它们的交点为I，求△ABI的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

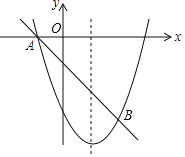
    【题目】如图，对称轴为x＝1的抛物线经过A（﹣1，0），B（2，﹣3）两点．

    （1）求抛物线的解析式；

    （2）P是抛物线上的动点，连接PO交直线AB于点Q，当Q是OP中点时，求点P的坐标；

    （3）C在直线AB上，D在抛物线上，E在坐标平面内，以B，C，D，E为顶点的四边形为正方形，直接写出点E的坐标．

    查看答案和解析>>

    同步练习册答案