
����Ŀ��ij����һ����������״�Ĺ۾�����ABC����������ͼ��ʾ����ͼ�н�����ֱ������ϵ�У������ߵĽ���ʽΪy=��![]() +c�ҹ�����C��0��5�������ȵ�λ��m��
+c�ҹ�����C��0��5�������ȵ�λ��m��
��1��ֱ��д��c��ֵ��
��2�������������ƻ��ع��ŵ�̨�ױ�������һ������Ϊ1.5m�ĵ�̺����̺�ļ۸�Ϊ20Ԫ/m2�������̺�����Ԫ��
��3���ڹ��żӹ�ά��ʱ����ġ����ּܡ�Ϊ����EFGH��H��G�ֱ��������ߵ����Ҳ��ϣ���������б��EG����֪����EFGH���ܳ�Ϊ27.5m����б��EG����б����GEF�Ķ���������ȷ��0.1�㣩

���𰸡�(1)5����2��900Ԫ����3��20.6��.
��������
��1�����ݵ����������������c��
��2�����ݽ���ʽ���A��B��C�������꣬�����̺���ܳ��ȣ��ٸ��ݵ�̺�ļ۸���������̺��Ҫ��Ǯ��
��3������֪����EFGH���ܳ������GF��EF�ߵij��ȣ��ٸ������Ǻ������������б�ǡ�GEF�Ķ�����
��1�������ߵĽ���ʽΪy=��![]() +c��
+c��
�ߵ㣨0��5������������
��c=5��
��2���ɣ�1��֪��OC=5��
��y=0������![]() +5=0�����x1=10��x2=��10��
+5=0�����x1=10��x2=��10��
���̺���ܳ���Ϊ��AB+2OC=20+2��5=30��
��30��1.5��20=900
�𣺹����̺��Ҫ900Ԫ��
��3������G��������m����![]() +5������m��0
+5������m��0
��EF=2m��GF=��![]() +5��
+5��
����֪�ã�2��EF+GF��=27.5��
��2��2m��![]() +5��=27.5��
+5��=27.5��
��ã�m1=5��m2=35���������⣬��ȥ����
��m1=5���룬��![]() +5=��
+5=��![]() ��52+5=3.75��
��52+5=3.75��
���G�������ǣ�5��3.75����
��EF=10��GF=3.75��
��Rt��EFG��tan��GEF=![]() =0.375��
=0.375��
���GEF��20.6�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC=4����BAC=90������D�ڱ�AB�ϣ�BE��CD��AE��CD������ΪF����EF=2����G���߶�CF�ϣ�����GAF=45��������ACG�����Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������μ����е���̨��֯�ġ�ĵ���������������Ŀ��������������ѡ���˳��ͨ�أ���һ����ѡ����3��ѡ��ڶ�����ѡ����4��ѡ��������������ᣬ����������������������������(ʹ�á�������һ�ο�����������ȥ������һ���һ������ѡ��)��
(1)����������Ρ����������ڵ�һ������ʹ�ã���ô����ͨ�صĸ�����________��
(2)����������Ρ����������ڵڶ�������ʹ�ã���ô����ͨ�صĸ�����________��
(3)�������ÿ�������һ�Ρ���������������״ͼ�����б���������˳��ͨ�صĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵ�У�![]() �Ķ��㶼��������ϣ����У�C������Ϊ
�Ķ��㶼��������ϣ����У�C������Ϊ![]() ��
��
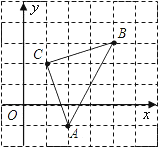
��1��д����A��B�����꣺
![]() ______ ��______
______ ��______ ![]() ��
��![]() ______ ��______
______ ��______ ![]()
��2����![]() ������ƽ��2����λ���ȣ�������ƽ��1����λ���ȣ��õ�
������ƽ��2����λ���ȣ�������ƽ��1����λ���ȣ��õ�![]() ����
����![]() ��������������ֱ���
��������������ֱ���![]() ______ ��______
______ ��______ ![]() ��
��![]() ______ ��______
______ ��______ ![]() ��
��![]() ______ ��______
______ ��______ ![]()
��3����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ��
��![]() ��������С����λ�ó������Σ��־���������С��֮����һ�����ﳬ�У�ʹ���е�����С���ľ�����ȣ�����Ӧ���ڣ� ��
��������С����λ�ó������Σ��־���������С��֮����һ�����ﳬ�У�ʹ���е�����С���ľ�����ȣ�����Ӧ���ڣ� ��

A.�ڡ�A����B���ڽ�ƽ���ߵĽ��㴦
B.��AC��BC���ߴ�ֱƽ���ߵĽ��㴦
C.��AC��BC���߸��ߵĽ��㴦
D.��AC��BC�������ߵĽ��㴦
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
���ǿ���ͨ�����в������![]() �Ĵ�С��
�Ĵ�С��
��һ������Ϊ12=1��22=4��1��2��4������1��![]() ��2��
��2��
�ڶ�����ͨ��ȡ1��2��ƽ������С![]() ���ڵķ�Χ��ȡ
���ڵķ�Χ��ȡ![]() ��
��
��Ϊ1.52=2.25��2��2.25������1��![]() ��1.5��
��1.5��
��1������յ�һ����ͨ�����㣬ȷ��![]() �������������ڵ�����֮�䣿
�������������ڵ�����֮�䣿
��2����1��![]() ��1.5�Ļ����ϣ��ظ�Ӧ�õڶ�����ȡƽ�����ķ�������
��1.5�Ļ����ϣ��ظ�Ӧ�õڶ�����ȡƽ�����ķ�������![]() ���ڵķ�Χ��С��m��
���ڵķ�Χ��С��m��![]() ��n��ʹ��n��m=
��n��ʹ��n��m=![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС����ҵʵ�й�����ҵ���ҹ��ƶȣ����˹��ʷ�ΪA��B��C��D�ĸ����Σ�С���Ը���ҵ���·ݹ��˹��ʽ��е��飬�������ռ��������ݣ������������в�������ͳ�Ʊ�������ͳ��ͼ��
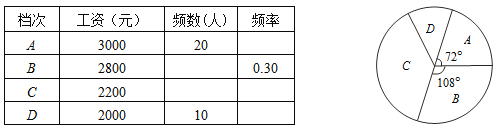
���������ṩ����Ϣ���ش��������⣺
��1�������ҵ���ж����ˣ�
��2���뽫ͳ�Ʊ�����������
��3������ͳ��ͼ�С�C���Ρ����������Ե�Բ�Ľ��� ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���õؿ�չ����ͳ�Ļ���У������������˲���ѧ�����˽�������ϲ���Ĵ�ͳ�Ļ���Ŀ���ͣ���Ϊ�鷨��Χ�塢Ϸ�硢������4�ࣩ������ͳ�ƽ�����Ƴ���ͼ��������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
��ϲ���Ĵ�ͳ�Ļ���Ŀ����Ƶ���ֲ���


����������Ϣ����������⣺
��1��ֱ��д��Ƶ���ֲ�����a��ֵ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����ȫУ����ѧ��1500�������Ƹ�У��ϲ��Χ���ѧ����Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���B���C��ƽ���߽��ڵ�O������O��DE��BC���ֱ�AB��AC�ڵ�D��E����AB��5��AC��4�����ADE���ܳ���______
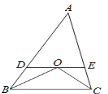
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com