
【题目】如图,在△ABC中,AB=AC=4,∠BAC=90°,点D在边AB上,BE∥CD,AE⊥CD,垂足为F,且EF=2,点G在线段CF上,若∠GAF=45°,则△ACG的面积为_____.

【答案】![]() ﹣1
﹣1
【解析】
首先证明△CAF≌△ABE,推出AE=CF,设AF=x,则CF=AE=x+2,在Rt△ACF中,根据AC2=AF2+CF2,可得42=x2+(x+2)2,求出x即可解决问题;
∴∠AFD=∠AEB=∠AFC=90,
∴∠CAF+∠EAB=90,∠EAB+∠ABE=90,
∴∠CAF=∠ABE,
∵AC=AB,
∴△CAF≌△ABE,
∴AE=CF,设AF=x,则CF=AE=x+2,
在Rt△ACF中,∵AC2=AF2+CF2,
∴42=x2+(x+2)2,
∴x=1+![]() 或1
或1![]() (舍弃)
(舍弃)
∵∠GAF=45,∠AFG=90
∴AF=FG=![]() 1,CG=CFFG=1+
1,CG=CFFG=1+![]() (
(![]() 1)=2,
1)=2,
∴S△AGC=![]() CGAF=
CGAF=![]() 1,
1,
故答案为:![]() ﹣1
﹣1


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
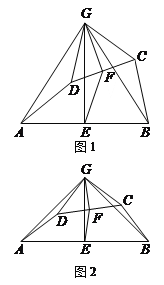
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
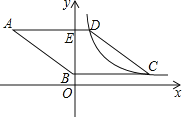
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
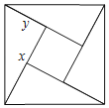
【题目】如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边
表示直角三角形的两直角边![]() ,下列四个说法:①
,下列四个说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中说法正确的是
;其中说法正确的是![]()
![]()
A. ①②B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里:
![]() ,2.525525552…(相邻两个2之间的5的个数逐个加1),0,
,2.525525552…(相邻两个2之间的5的个数逐个加1),0,![]() ,
,![]() ,0.12,
,0.12,![]() ,
,![]() ,
,![]() ,
,![]()
(1)负数集合:{ …};
(2)非负整数集合:{ …};
(3)分数集合:{ …};
(4)无理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
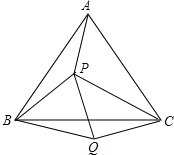
【题目】如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后解决后面的问题.
材料:一个三位数![]() (百位数为a,十位数为b,个位数为c),若a+c=b,则称这个三整数
(百位数为a,十位数为b,个位数为c),若a+c=b,则称这个三整数![]() 为“协和数”,同时规定c=
为“协和数”,同时规定c=![]() (k≠0),k称为“协和系数”,如264,因为它的百位上数字2与个位数字4之和等于十位上的数字6,所有264是“协和数”,则“协和数”k=2×4=8.
(k≠0),k称为“协和系数”,如264,因为它的百位上数字2与个位数字4之和等于十位上的数字6,所有264是“协和数”,则“协和数”k=2×4=8.
(1)对于“协和数”![]() ,求证:“协和数”
,求证:“协和数”![]() 能被11整除.
能被11整除.
(2)已知有两个十位数相同的“协和数”![]() ,
,![]() (a1>a2),且k1﹣k2=1,若y=k1+k2,用含b的式子表示y.
(a1>a2),且k1﹣k2=1,若y=k1+k2,用含b的式子表示y.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
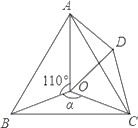
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=﹣![]() +c且过顶点C(0,5)(长度单位:m)
+c且过顶点C(0,5)(长度单位:m)
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5m的地毯,地毯的价格为20元/m2,求购买地毯需多少元?
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求斜面EG的倾斜角∠GEF的度数.(精确到0.1°)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com