
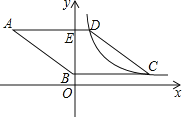
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,点E是BC延长线上的一点,且BD=DE.点G是线段BC的中点,连结AG,交BD于点F,过点D作DH⊥BC,垂足为H.
(1)求证:△DCE为等腰三角形;
(2)若∠CDE=22.5°,DC=![]() ,求GH的长;
,求GH的长;
(3)探究线段CE,GH的数量关系并用等式表示,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,记
中,记![]() ,
,![]() .
.
(1)如图![]() ,若
,若![]() 平分
平分![]() ,
,![]() 、
、![]() 分别是
分别是![]() 的外角
的外角![]() 和
和![]() 的平分线,
的平分线,![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的度数,用含
的度数,用含![]() 的代数式表示
的代数式表示![]() 的度数,并说明理由.
的度数,并说明理由.

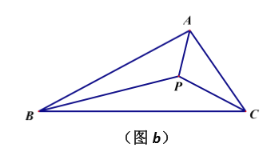
(2)如图![]() ,若点
,若点 ![]() 为
为![]() 的三条内角平分线的交点,
的三条内角平分线的交点,![]() 于点
于点 ![]() , 猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.
, 猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.
![]() .
.
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
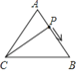
【题目】如图,点P是等边△ABC的边上的一个做匀速运动的动点,其由点A开始沿AB边运动到B再沿BC边运动到C为止,设运动时间为t,△ACP的面积为S,则S与t的大致图象是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c和直线y=x+1交于A,B两点,点A在x轴上,点B在直线x=3上,直线x=3与x轴交于点C

(1)求抛物线的解析式;
(2)点P从点A出发,以每秒![]() 个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
①当t为何值时,矩形PQNM的面积最小?并求出最小面积;
②直接写出当t为何值时,恰好有矩形PQNM的顶点落在抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
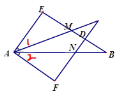
【题目】如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出的结论:①∠1=∠2;②BE=CF;③△CAN≌△BMA;④CD=DN,;其中正确的结论是___________________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH.
(1)若BC=12![]() ,AB=13,求AF的长;
,AB=13,求AF的长;
(2)求证:EB=EH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,∠BAC=90°,点D在边AB上,BE∥CD,AE⊥CD,垂足为F,且EF=2,点G在线段CF上,若∠GAF=45°,则△ACG的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;
(3)如果锐锐每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com