
【题目】如图,点P是等边△ABC的边上的一个做匀速运动的动点,其由点A开始沿AB边运动到B再沿BC边运动到C为止,设运动时间为t,△ACP的面积为S,则S与t的大致图象是( )
A.  B.
B.  C.
C.  D.
D. 
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A观测站在B观测站的正东方向,有一艘小船在点P处,从A处测得小船在北偏西60°方向,从B处测得小船在北偏东45°的方向,点P到点B的距离是3![]() 千米.(注:结果有根号的保留根号)
千米.(注:结果有根号的保留根号)
(1)求A,B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向以![]() 千米/时的速度进行沿途考察,航行一段时间后到达点C处,此时,从B测得小船在北偏西15°方向,求小船沿途考察的时间.
千米/时的速度进行沿途考察,航行一段时间后到达点C处,此时,从B测得小船在北偏西15°方向,求小船沿途考察的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:

①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地相距
两地相距![]() ,甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由
,甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由![]() 地到达
地到达![]() 地.他们行驶的路程
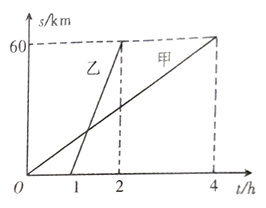
地.他们行驶的路程![]() 与甲出发后的时间
与甲出发后的时间![]() 之间的函数图像如图所示.
之间的函数图像如图所示.
(1)乙比甲晚出发几小时?乙比甲早到几小时?
(2)分别写出甲、乙行驶的路程![]() 与甲出发后的时间
与甲出发后的时间![]() 的函数关系式(不写自变量的取值范围).
的函数关系式(不写自变量的取值范围).
(3)乙在甲出发后几小时追上甲?追上甲的地点离![]() 地有多远?
地有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段![]()
求作:菱形![]() ,使得
,使得![]() 且
且![]() .
.
以下是小丁同学的作法:
①作线段![]() ;
;
②分别以点![]() ,
,![]() 为圆心,线段
为圆心,线段![]() 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点![]() ;
;
③再分别以点![]() ,
,![]() 为圆心,线段
为圆心,线段![]() 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点![]() ;
;
④连接![]() ,
,![]() ,
,![]() .
.
则四边形![]() 即为所求作的菱形.(如图)
即为所求作的菱形.(如图)
老师说小丁同学的作图正确.则小丁同学的作图依据是:_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.

∵EF∥AD,( )
∴∠2= .(两直线平行,同位角相等)
又∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实国家关于增强青少年体质的计划,我市全面实施了义务教育学段中小学学生“饮用奶计划”的营养工程.某牛奶供应商拟提供A(原味)、B(草莓味)、C(核桃味)、D(菠萝味)、E(香橙味)等五种口味的学生奶供学生选择(所有学生奶盒形状、大小相同),为了解对学生奶口味的喜好情况,某初级中学九年级(1)班张老师对全班同学进行了调查统计,制成了如图所示的两幅不完整的统计图.
(1)该班共有多少人?
(2)求出喜好A和E学生奶口味的人数;
(3)该班五种口味的学生奶喜好人数组成一组统计数据,求出这组数据的平均数;
(4)将折线统计图补充完整.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com