
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.

∵EF∥AD,( )
∴∠2= .(两直线平行,同位角相等)
又∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
【答案】(已知),(两直线平行,同位角相等),(已知),(等量代换),(内错角相等,两直线平行),(两直线平行,同旁内角互补),(已知),110°.
【解析】
试题推理填空题.本题主要考查了平行线的性质和判定定理等知识点,理解平行线的性质和判定定理是解此题的关键.根据题意,利用平行线的性质和判定填空即可.
试题解析:
解:∵EF∥AD(已知),
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3,(等量代换)
∴AB∥DG.(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°.(两直线平行,同旁内角互补)
又∵∠BAC=70°,(已知)
∴∠AGD=110°.


科目:初中数学 来源: 题型:
【题目】计算:
(1)4﹣8+6﹣10;
(2)(![]() ﹣
﹣![]() +
+![]() )×(﹣24);
)×(﹣24);
(3)(﹣2)2×5﹣(﹣2.5)÷0.5;
(4)﹣32+(﹣24)÷(﹣4)﹣(﹣3)3×(﹣![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试,计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,达到9分或10分为优秀,成绩如表1所示,并制作了成绩分析表(表2)
表1
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
表2
班级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
一班 | 7.6 | 8 | a | 3.82 | 70% | 30% |
二班 | b | c | 10 | 4.94 | 80% | 40% |
(1)求表2中,a,b,c;
(2)有人说二班的及格率、优秀率均高于一班,所以二班成绩比一班成绩好;但也有人坚定认为一班成绩比二班成绩好.请你给出支持一班成绩好的两条理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间的甲、乙两名工人分别同时生产同种零件,他们一天生产零件y(个)与生产时间t(小时)的关系如图所示.
(1)根据图象回答:
①甲、乙中,谁先完成一天的生产任务;在生产过程中,谁因机器故障停止生产多少小时;
②当t等于多少时,甲、乙所生产的零件个数相等;
(2)谁在哪一段时间内的生产速度最快?求该段时间内,他每小时生产零件的个数.
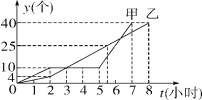
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两车间共120人,其中甲车间人数比乙车间人数的4倍少5人.
(1)求甲、乙两车间各有多少人?
(2)若从甲、乙两车间分别抽调工人,组成丙车间研制新产品,并使甲、乙、丙三个车间的人数比为13∶4∶7,那么甲、乙两车间要分别抽调多少工人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
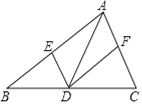
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明元旦前到文具超市用15元买了若干练习本,元旦这一天,该超市开展优惠活动,同样的练习本比元旦前便宜0.2元,小明又用20.7元钱买练习本,所买练习本的数量比上一次多50%,小明元旦前在该超市买了多少本练习本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量? 操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现定义新运算“△”,对于任意有理数a,b,都有a△b=a2-ab+b,例如:3△5=32-3×5+5=-1,请根据上述知识解决问题:
(1)化简:(x-1)△(2+x);
(2)若(1)中的代数式的值大于6而小于9,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com