
【题目】现定义新运算“△”,对于任意有理数a,b,都有a△b=a2-ab+b,例如:3△5=32-3×5+5=-1,请根据上述知识解决问题:
(1)化简:(x-1)△(2+x);
(2)若(1)中的代数式的值大于6而小于9,求x的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
(1)先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为 , 若A为随机事件,则m的取值为;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)|﹣3|﹣(![]() )﹣2+(
)﹣2+(![]() )0
)0
(2)(﹣3m2n)2(﹣2m2)÷6mn2
(3)2x(x﹣![]() y)﹣(x+2y)(x﹣y)
y)﹣(x+2y)(x﹣y)
(4)[(x﹣2y)2﹣x(x﹣4y)﹣8xy]÷4y
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,A(1,3),B(2,1),直角坐标系中存在点C,使得O,A,B,C四点构成平行四边形,则C点的坐标为______________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四幅图像分别表示变量之间的关系,请按图像的顺序,将下面的四种情境与之对应排序.

a.运动员推出去的铅球(铅球的高度与时间的关系);
b.静止的小车从光滑的斜面滑下(小车的速度与时间的关系);
c.一个弹簧由不挂重物到所挂重物的质量逐渐增加(弹簧的长度与所挂重物的质量的关系);
d.小明从A地到B地后,停留一段时间,然后按原来的速度原路返回(小明离A地的距离与时间的关系).
正确的顺序是( )
A. abcd B. abdc C. acbd D. acdb
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为 ![]() 的线段的概率为( )
的线段的概率为( )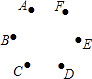
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.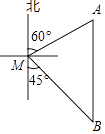
(1)求渔船从B到A的航行过程中与码头M之间的最小距离.
(2)若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com