
����Ŀ����ͼ���ķ�ͼ��ֱ��ʾ����֮��Ĺ�ϵ���밴ͼ���˳������������龳��֮��Ӧ����

a���˶�Ա�Ƴ�ȥ��Ǧ��(Ǧ��ĸ߶���ʱ��Ĺ�ϵ)��
b����ֹ��С���ӹ⻬��б�滬��(С�����ٶ���ʱ��Ĺ�ϵ)��
c��һ�������ɲ������ﵽ�������������������(���ɵij�������������������Ĺ�ϵ)��
d��С����A�ص�B�غ�ͣ��һ��ʱ�䣬Ȼ��ԭ�����ٶ�ԭ·����(С����A�صľ�����ʱ��Ĺ�ϵ)��
��ȷ��˳����(����)
A. abcd B. abdc C. acbd D. acdb
���𰸡�D
��������
����������ͼ����һ�κ���ͼ���Ƿֶκ���ͼ��������������ͼ��
a���˶�Ա�Ƴ�ȥ��Ǧ����˶��켣�������ߣ���������ʾ��ͼ�Σ�
b����ֹ��С���ӹ⻬��б�滬�£�С�����ٶȻ���0�Ļ����ϣ�����ʱ��ı仯Խ��Խ�죬��������ʾ��ͼ��
c��һ�������ɲ������ﵽ������������������ӣ����ɵij��Ȼ�����������������������Ӷ��䳤����Ϊ�����쳤�ij�������ԭ�е��ɳ��ȵĻ����ϱ仯�ģ���ѡ�ڣ�
d��С����A�ص�B����һ���̣�С����A�صľ��������ʱ������������ӣ��ڡ�ͣ��һ��ʱ�䡱��������У�С����A�صľ��벻��仯���ڡ�ԭ�ٶ�ԭ·���ء��Ĺ����У�С����A�صľ��������ʱ�����������С��һֱ���ص�ԭ�أ����۵�ͼ��
��ѡD��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������l1��y=��x2+2x+3��x�ύ�ڵ�A��B����A�ڵ�B��ߣ�����y�ύ�ڵ�C��������l2������A����x�����һ������ΪE��4��0������y�ύ�ڵ�D��0����2����
��1����������l2�Ľ���ʽ��
��2����PΪ�߶�AB��һ���㣨����A��B�غϣ�������P��y���ƽ���߽�������l1�ڵ�M����������l2�ڵ�N��
�ٵ��ı���AMBN��������ʱ�����P�����ꣻ
�ڵ�CM=DN��0ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���̵�����ŵ�������Ҫװ�ޣ�װ���ڼ���ͣӪҵ�������������װ����ͬʱʩ����8�������ɣ��踶���ù�3520Ԫ����������鵥����6�죬�������鵥����12�������ɣ��踶����3480Ԫ���ʣ�
��1���ס������鹤��һ�죬�̵��Ӧ������Ǯ��
��2����֪���鵥�������12�죬���鵥�������24�죬�������ĸ��飬�̵�����������٣�
��3��װ����ϵڶ��켴������Ӫҵ����ÿ���Կ�ӯ��200Ԫ(��װ��ǰ��ÿ��ӯ������)������Ϊ�̵�Ӧ��ΰ���ʩ����������˵˵������ɣ�(���ã�1����2���ʵ�����������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
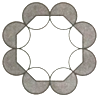
����Ŀ����ͼ���Ѱ˸���Բ�������������аڷţ���Բ�����߹���һ�����˱��Σ������˱����ڲ�˸����Σ�����Ӱ���֣����֮��ΪS1 �� ���˱������˸����Σ���Ӱ���֣����֮��ΪS2 �� �� ![]() =�� ��
=�� ��
A.![]()
B.![]()
C.![]()
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֶ��������㡰��������������������a��b������a��b��a2��ab��b�����磺3��5��32��3��5��5����1�����������֪ʶ������⣺
(1)����(x��1)��(2��x)��
(2)��(1)�еĴ���ʽ��ֵ����6��С��9����x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
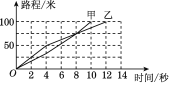
����Ŀ���ס������˽��б�����·����ʱ��Ĺ�ϵ��ͼ��ʾ��
(1)����һ��________�ױ�����
(2)ǰһ��������________���ٶȽϿ죬����________Ӯ���˱�����
(3)���˵�________����;������������ʱ���յ�________�ף�
(4)����ǰ8���ƽ���ٶ��Ƕ��٣������������̵�ƽ���ٶ��Ƕ��٣�����ǰ8���ƽ���ٶ��Ƕ��٣������������̵�ƽ���ٶ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���B��ƽ����BE��AD���ڵ�E����BED��ƽ����EF��DC���ڵ�F����AB=9��DF=2FC����BC= �� ������������ţ�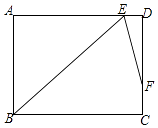
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ��ֱ��뷴��������y= ![]() ��ͼ���ڵ�һ�����ڵ�A��4��3������y��ĸ����ύ�ڵ�B����OA=OB��
��ͼ���ڵ�һ�����ڵ�A��4��3������y��ĸ����ύ�ڵ�B����OA=OB��
��1������y=kx+b��y= ![]() �ı���ʽ��
�ı���ʽ��
��2����֪��C��0��5�������ڸ�һ�κ���ͼ����ȷ��һ��M��ʹ��MB=MC�����ʱ��M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣨ ![]() ����1+
����1+ ![]() +sin30�㣻
+sin30�㣻
��1�����㣺�� ![]() ����1+
����1+ ![]() +sin30�㣻
+sin30�㣻
��2���Ȼ�������ֵ����m+2����m��2������m��2��2+1������m=2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com