
【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A,B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).
(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.
【答案】
(1)解:∵令﹣x2+2x+3=0,解得:x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0).
设抛物线l2的解析式为y=a(x+1)(x﹣4).
∵将D(0,﹣2)代入得:﹣4a=﹣2,
∴a= ![]() .
.
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣2
x﹣2
(2)解:①如图1所示:

∵A(﹣1,0),B(3,0),
∴AB=4.
设P(x,0),则M(x,﹣x2+2x+3),N(x, ![]() x2﹣
x2﹣ ![]() x﹣2).
x﹣2).
∵MN⊥AB,
∴SAMBN= ![]() ABMN=﹣3x2+7x+10(﹣1<x<3).
ABMN=﹣3x2+7x+10(﹣1<x<3).
∴当x= ![]() 时,SAMBN有最大值.
时,SAMBN有最大值.
∴此时P的坐标为( ![]() ,0).
,0).
②如图2所示:作CG⊥MN于G,DH⊥MN于H,如果CM与DN不平行.

∵DC∥MN,CM=DN,
∴四边形CDNM为等腰梯形.
∴∠DNH=∠CMG.
在△CGM和△DNH中 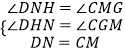 ,
,
∴△CGM≌△DNH.
∴MG=HN.
∴PM﹣PN=1.
设P(x,0),则M(x,﹣x2+2x+3),N(x, ![]() x2﹣
x2﹣ ![]() x﹣2).
x﹣2).
∴(﹣x2+2x+3)+( ![]() x2﹣
x2﹣ ![]() x﹣2)=1,解得:x1=0(舍去),x2=1.
x﹣2)=1,解得:x1=0(舍去),x2=1.
∴P(1,0).
当CM∥DN时,如图3所示:

∵DC∥MN,CM∥DN,
∴四边形CDNM为平行四边形.
∴DC=MN.=5
∴﹣x2+2x+3﹣( ![]() x2﹣
x2﹣ ![]() x﹣2)=5,
x﹣2)=5,
∴x1=0(舍去),x2= ![]() ,
,
∴P( ![]() ,0).
,0).
总上所述P点坐标为(1,0),或( ![]() ,0).
,0).
【解析】1、直线l2经过A、D、E三点,只需求出A点坐标,就可以求出直线l2的解析式;2、①四边形AMBN的对角线互相垂直,SAMBN![]() ABMN,由A、B两点坐标求出线段AB的长,MN⊥AB得出点P、M、N三点的横坐标相同,设P(x,0),可以表示出点M、N的坐标,从而列出s与x的函数关系式,求得s的最大值时,x的值,于是就可以求得点P的坐标;②当CM=DN≠0时,分两种情况,当CM∥DN时四边形CDNM为平行四边形;当CM不平行 DN时,四边形CDNM为等腰梯形.就可以求出点P的坐标。
ABMN,由A、B两点坐标求出线段AB的长,MN⊥AB得出点P、M、N三点的横坐标相同,设P(x,0),可以表示出点M、N的坐标,从而列出s与x的函数关系式,求得s的最大值时,x的值,于是就可以求得点P的坐标;②当CM=DN≠0时,分两种情况,当CM∥DN时四边形CDNM为平行四边形;当CM不平行 DN时,四边形CDNM为等腰梯形.就可以求出点P的坐标。


 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,
,![]() ,则
,则![]() 和
和![]() 都是“和谐分式”.
都是“和谐分式”.
(1)下列分式中,不属于“和谐分式”的是 (填序号).
①![]() ②
②![]() ③
③![]() ④
④![]()
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式.
化成一个整式与一个分子为常数的分式的和的形式.
(3)应用:先化简![]() ,并求
,并求![]() 取什么整数时,该式的值为整数.
取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连结CQ.若PA∶PB∶PC=3∶4∶5,连结PQ,试判断△PQC的形状( )

A. 直角三角形 B. 等腰三角形 C. 锐角三角形 D. 钝角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为____cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
(1)先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为 , 若A为随机事件,则m的取值为;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B. 如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C. 若三角形三边长的比为1:2:3,则这个三角形是直角三角形
D. 如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四幅图像分别表示变量之间的关系,请按图像的顺序,将下面的四种情境与之对应排序.

a.运动员推出去的铅球(铅球的高度与时间的关系);
b.静止的小车从光滑的斜面滑下(小车的速度与时间的关系);
c.一个弹簧由不挂重物到所挂重物的质量逐渐增加(弹簧的长度与所挂重物的质量的关系);
d.小明从A地到B地后,停留一段时间,然后按原来的速度原路返回(小明离A地的距离与时间的关系).
正确的顺序是( )
A. abcd B. abdc C. acbd D. acdb
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com