
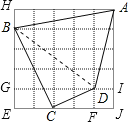
【题目】如图,在5×5的方格纸中,每一个小正方形的边长都为1.
(1)∠BCD是不是直角?请说明理由;
(2)求四边形ABCD的面积.

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)连接BD,由于每一个小正方形的边长都为1,根据勾股定理可分别求出△BCD的三边长,根据勾股定理的逆定理即可判断出△BCD的形状;
(2)S四边形ABCD=S正方形AHEJ-S△BCE-S△ABH-S△ADI-S△DCF-S正方形DFJI.
试题解析:(1)∠BCD是直角,理由如下:连接BD,
∵BC=![]() =2
=2![]() ,CD=
,CD=![]() =
=![]() ,BD=
,BD=![]() =5,
=5,
∴BC2+CD2=BD2,
∴∠BCD为直角;
(2)S四边形ABCD=S正方形AHEJ-S△BCE-S△ABH-S△ADI-S△DCF-S正方形DFJI,
所以S四边形ABCD=5×5﹣![]() ×4×2﹣
×4×2﹣![]() ×2×1﹣1×1﹣
×2×1﹣1×1﹣![]() ×4×1﹣
×4×1﹣![]() ×5×1,
×5×1,
=25﹣4﹣1﹣1﹣2﹣![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
A.a>0
B.3是方程ax2+bx+c=0的一个根
C.a+b+c=0
D.当x<1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A,B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).
(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点F是对角线BD上的一点,EF∥AB交AD于点E,FG∥BC交DC于点G,四边形EFGP是平行四边形,给出如下结论:
①四边形EFGP是菱形;
②△PED为等腰三角形;
③若∠ABD=90°,则△EFP≌△GPD;
④若四边形FPDG也是平行四边形,则BC∥AD且∠CDA=60°.
其中正确的结论的序号是(把所有正确结论的序号都填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
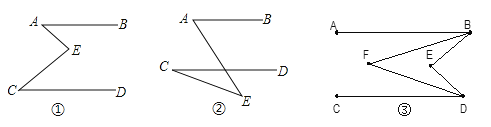
【题目】(1)如图①、②,AB∥CD,你能说明∠A、∠E、∠C的关系吗?(请在图形下的横线上写出其关系并选一个进行说明)
(2)如图③若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=80,则∠BFD=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△DEF是△ABC经过平移得到的.已知∠A=54°,∠ABC=36°,则下列结论不一定成立的是( )

A. ∠F=90° B. ∠BED=∠FED C. BC⊥DF D. DF∥AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
(3)装修完毕第二天即可正常营业,且每天仍可盈利200元(即装修前后每天盈利不变),你认为商店应如何安排施工更有利?说说你的理由.(可用(1)(2)问的条件及结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)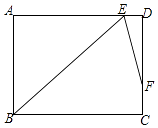
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com