
����Ŀ����ͼ�����ı���ABCD�У���֪AB=BC=CD����BAD�͡�CDA��Ϊ��ǣ���F�ǶԽ���BD�ϵ�һ�㣬EF��AB��AD�ڵ�E��FG��BC��DC�ڵ�G���ı���EFGP��ƽ���ı��Σ��������½��ۣ�
���ı���EFGP�����Σ�
�ڡ�PEDΪ���������Σ�
������ABD=90�㣬���EFP�ա�GPD��
�����ı���FPDGҲ��ƽ���ı��Σ���BC��AD�ҡ�CDA=60�㣮
������ȷ�Ľ��۵����������������ȷ���۵���Ŷ����ں����ϣ���
���𰸡��٢ۢ�
���������⣺��EF��AB��
�� ![]() =
= ![]() ��
��
��FG��BC��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��AB=BC��
��EF=FG��
���ı���EFGP��ƽ���ı��Σ�
���ı���EFGP�����Σ��ʢ���ȷ��
��BC=CD��
���DBC=��BDC��
��FG��BC��
���DBC=��DFG��
���DFG=��BDC��
��FG=DG��
��PG=FG=PE��
��PG=DG��
����֤�á�PDG�ǵȱ������Σ�
��PD��һ������PE��
���PED��һ���ǵ��������Σ��ʢڴ���
�ߡ�ABD=90�㣬PG��EF��
��PG��BD��
��FG=DG��
���FGP=��DGP��
���ı���EFGP��ƽ���ı��Σ�
���PEF=��FGP��
���DGP=��PEF��
�ڡ�EFP�͡�GPD��

���EFP�ա�GPD��SAS�����ʢ���ȷ��
���ı���FPDGҲ��ƽ���ı��Σ�
��FG��PD��
��FG��EP��
��E��P��D��һ��ֱ���ϣ�
��FG��BC��PE��
��BC��AD��
���ı���FPDGҲ��ƽ���ı��Σ�
��FG=PD��
��FG=DG=PG��
��PG=PD=DG��
���PGD�ǵȱ������Σ�
���CDA=60�㣮
���ı���ABCD��Ӧ����BC��AD����CDA=60�㣮�ʢ���ȷ��
���Դ��Ǣ٢ۢܣ�
�����㾫�����������⣬������Ҫ�˽����ε��ж�����(����һ���ı��Σ��ı���ȳ����Σ��ı��εĶԽ��ߣ���ֱ���������Σ���֪ƽ���ı��Σ��ڱ���Ƚ����Σ����Խ�������ֱ��˳������Ϊ����)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OABC�ı߳�Ϊ2��OA��x�Ḻ����ļн�Ϊ15�㣬��B��������y=ax2��a��0����ͼ���ϣ���a��ֵΪ�� ��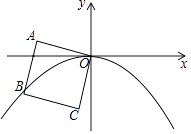
A.![]()
B.![]()
C.��2
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,����ABC��,��A=90��,��D��BC���е�,��E,F�ֱ���AB,AC��,����EDF=90��,����EF,��֤:BE2+CF2=EF2.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�����װ�н���ɫ��ͬ��5��С�����к���3��������2����
��1���ȴӴ���ȡ��m��m��1���������ٴӴ������������1��������������Ϊ�¼�A����գ���AΪ��Ȼ�¼�����m��ֵΪ �� ��AΪ����¼�����m��ȡֵΪ��
��2�����Ӵ����������2�������ú������1����������¼��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��y�Ķ�Ԫһ�η�����![]() �Ľ���һ�����������ε�һ������һ���ױߵij�����������������ε��ܳ�Ϊ9����m��ֵ��
�Ľ���һ�����������ε�һ������һ���ױߵij�����������������ε��ܳ�Ϊ9����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����5��5�ķ���ֽ�У�ÿһ��С�����εı߳���Ϊ1��
��1����BCD�Dz���ֱ�ǣ���˵�����ɣ�
��2�����ı���ABCD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
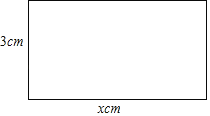
����Ŀ����ͼ����֪�������������ߵij��ֱ���xcm��3cm���賤���ε����Ϊycm2��
��1����д�������ε����y��x֮��Ĺ�ϵʽ��
��2�����ã�1���еĹ�ϵʽ����x��5cmʱ�����ε������
��3����x��ֵ��4cm�仯��12cmʱ�������ε�������� ��cm2�仯���� ��cm2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣮
��1��|��3|����![]() ����2+��
����2+��![]() ��0
��0
��2������3m2n��2����2m2����6mn2
��3��2x��x��![]() y������x+2y����x��y��
y������x+2y����x��y��
��4��[��x��2y��2��x��x��4y����8xy]��4y
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��B��C��D��E��F�DZ߳�Ϊ1���������εĶ��㣬��������������ɵõ�һ���߶Σ��������������õ������߶�����ȡһ���߶Σ�ȡ������Ϊ ![]() ���߶εĸ���Ϊ�� ��
���߶εĸ���Ϊ�� ��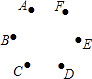
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com