
【题目】在△ABC中,∠B=45°,点D在边BC上,AD=AC,点E在边AD上,∠BCE=45°,若AB=5 ![]() .AE=2DE,则AC= .
.AE=2DE,则AC= . 
【答案】![]()
【解析】解:过A作AM⊥BC于M,过作EN∥AB交BC于N,
则△DEN∽△DAB,∴∠ENC=∠B=45°,
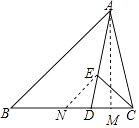
∴△ABM与△ENC是等腰直角三角形,
∵AB=5 ![]() ,
,
∴AM=BM=5,
∵DE:AE= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴NE= ![]() ,
,
∴NC= ![]() ,
,
设CM=x,则CD=2x,ND=NC﹣CD= ![]() ﹣2x,BO=5﹣x,
﹣2x,BO=5﹣x,
则 ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴x=1,∴CM=1,
∴AC= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
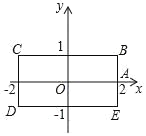
【题目】如图,长方形 BCDE 的各边分别平行于 x 轴或 y 轴,物体甲和物体乙分别由点 A(2,0)同时出发,沿长方形 BCDE 的边作环绕运动,物体甲按逆时针方向以 1 个单位/秒匀速运动,物体乙按顺时针方向以 2 个单位/秒匀速运动,则两个物体运动后的第 2020 次相遇地点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A,B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).
(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
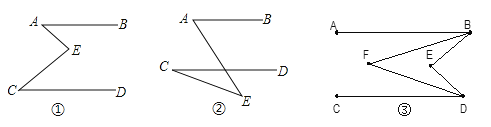
【题目】(1)如图①、②,AB∥CD,你能说明∠A、∠E、∠C的关系吗?(请在图形下的横线上写出其关系并选一个进行说明)
(2)如图③若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=80,则∠BFD=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△DEF是△ABC经过平移得到的.已知∠A=54°,∠ABC=36°,则下列结论不一定成立的是( )

A. ∠F=90° B. ∠BED=∠FED C. BC⊥DF D. DF∥AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将方格纸中的△ABC向上平移4个单位长度,然后向右平移6个单位长度,得到△A1B1C1.
(1)画出平移后的图形;
(2)线段AA1,BB1的位置关系是______;数量关系是________.
(3)如果每个方格的边长是1,那么△ABC的面积是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
(3)装修完毕第二天即可正常营业,且每天仍可盈利200元(即装修前后每天盈利不变),你认为商店应如何安排施工更有利?说说你的理由.(可用(1)(2)问的条件及结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
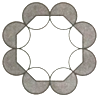
【题目】如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1 , 正八边形外侧八个扇形(阴影部分)面积之和为S2 , 则 ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com