练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：

    （1）4﹣8+6﹣10；

    （2）（﹣+）×（﹣24）；

    （3）（﹣2）2×5﹣（﹣2.5）÷0.5；

    （4）﹣32+（﹣24）÷（﹣4）﹣（﹣3）3×（﹣）．

    【答案】（1）-8；（2）-14；（3）25；（4）-21.

    【解析】

    （1）直接计算加减即可；（2）利用乘法分配律，用括号里的每一项分别乘以-24，再求和即可；(3)先算乘方，后算乘除，最后算加减即可；(4) 先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．

    （1）原式＝（4+6）+（﹣8﹣10）

    ＝10+（﹣18）

    ＝﹣8；

    （2）原式＝×（﹣24）﹣×（﹣24）+×（﹣24）

    ＝﹣12+18﹣20

    ＝﹣14；

    （3）原式＝4×5﹣（﹣5）

    ＝20+5

    ＝25；

    （4）原式＝﹣9+6﹣（﹣27）×（﹣）

    ＝﹣3﹣18

    ＝﹣21．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】2018年俄罗斯世界杯组委会对世界杯比赛用球进行抽查，随机抽取了100个足球，检测每个足球的质量是否符合标准，超过或不足部分分别用正、负数来表示，记录如表：

    与标准质量的差值（单位：克）

    ﹣4

    ﹣2

    0

    1

    3

    6

    个数

    10

    13

    30

    25

    15

    7

    （1）平均每个足球的质量比标准质量多还是少？用你学过的方法合理解释；

    （2）若每个足球标准质量为420克，则抽样检测的足球的总质量是多少克？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】武汉市光谷实验中学九（1）班为了了解全班学生喜欢球类活动的情况，采取全面调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），下列说法错误的是（　　）

    A. 九（1）班的学生人数为40 B. m的值为10

    C. n的值为20 D. 表示“足球”的扇形的圆心角是70°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（﹣4，0），点B的坐标是（0，b）（b＞0）．P是直线AB上的一个动点，作PC⊥x轴，垂足为C．记点P关于y轴的对称点为P′（点P′不在y轴上），连接PP′，P′A，P′C．设点P的横坐标为a．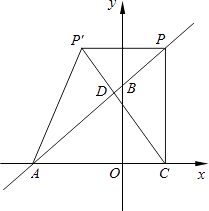
    （1）当b=3时， ①求直线AB的解析式；
    ②若点P′的坐标是（﹣1，m），求m的值；
    （2）若点P在第一象限，记直线AB与P′C的交点为D．当P′D：DC=1：3时，求a的值；
    （3）是否同时存在a，b，使△P′CA为等腰直角三角形？若存在，请求出所有满足要求的a，b的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CD是⊙O的直径，弦AB⊥CD，垂足为点M，AB=20，分别以CM、DM为直径作两个大小不同的 ⊙O1和⊙O2 ， 则图中阴影部分的面积为（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列各式：定义一种新运算“⊙”：

    1⊙3＝1×4+3＝7，3⊙﹣1＝3×4﹣1＝11，5⊙4＝5×4+4＝24

    4⊙（﹣3）＝4×4﹣3＝13，（﹣2）⊙（﹣5）＝（﹣2）×4﹣5＝﹣13，……

    （1）写出一般结论：a⊙b＝_____；

    （2）如果a≠b，那么a⊙b_____b⊙a（填“＝”或“≠”）

    （3）先化简，再求值：（a﹣b）⊙（2a+3b）．其中a＝﹣，b＝2019．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

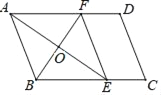
    【题目】如图，在平行四边形ABCD中，∠BAD的平分线交BC于E，点F在AD上，且AF=AB，连接EF．

    （1）判断四边形ABEF的形状并证明；

    （2）若AE、BF相交于点O，且四边形ABEF的周长为20，BF=6，求AE的长度及四边形ABEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小敏从A地出发向B地行走，同时小聪从B地出发向A地行走，如图所示，相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y（km）与已用时间x（h）之间的关系，则小敏、小聪行走的速度分别是（ ）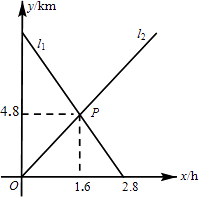
    A.3km/h和4km/h
    B.3km/h和3km/h
    C.4km/h和4km/h
    D.4km/h和3km/h

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，EF∥AD，∠1＝∠2，∠BAC＝70°．将求∠AGD的过程填写完整．

    ∵EF∥AD，（　 　）

    ∴∠2＝　 　．（两直线平行，同位角相等）

    又∵∠1＝∠2，（　 　）

    ∴∠1＝∠3．（　 　）

    ∴AB∥DG．（　 　）

    ∴∠BAC+　 　＝180°（　 　）

    又∵∠BAC＝70°，（　 　）

    ∴∠AGD＝　 　．

    查看答案和解析>>

    同步练习册答案