
【题目】如图,抛物线y=﹣x2+bx+c和直线y=x+1交于A,B两点,点A在x轴上,点B在直线x=3上,直线x=3与x轴交于点C

(1)求抛物线的解析式;
(2)点P从点A出发,以每秒![]() 个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
①当t为何值时,矩形PQNM的面积最小?并求出最小面积;
②直接写出当t为何值时,恰好有矩形PQNM的顶点落在抛物线上.
【答案】(1)抛物线解析式为y=﹣x2+3x+4;(2)①当t=![]() 时,面积最小是
时,面积最小是![]() ;②t=
;②t=![]() 、
、![]() 或2.
或2.
【解析】
(1)利用待定系数法进行求解即可;
(2)①分别用t表示PE、PQ、EQ,用△PQE∽△QNC表示NC及QN,列出矩形PQNM面积与t的函数关系式问题可解;
②由①利用线段中点坐标分别等于两个端点横纵坐标平均分的数量关系,表示点M坐标,分别讨论M、N、Q在抛物线上时的情况,并分别求出t值.
(1)由已知,B点横坐标为3,
∵A、B在y=x+1上,
∴A(﹣1,0),B(3,4),
把A(﹣1,0),B(3,4)代入y=﹣x2+bx+c得,
![]() ,解得:
,解得:![]() ,
,
∴抛物线解析式为y=﹣x2+3x+4;
(2)①如图,过点P作PE⊥x轴于点E,
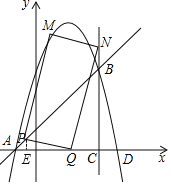
∵直线y=x+1与x轴夹角为45°,P点速度为每秒![]() 个单位长度,
个单位长度,
∴t秒时点E坐标为(﹣1+t,0),Q点坐标为(3﹣2t,0),
∴EQ=4﹣3t,PE=t,
∵∠PQE+∠NQC=90°,
∠PQE+∠EPQ=90°,
∴∠EPQ=∠NQC,
∴△PQE∽△QNC,
∴![]() ,
,
∴矩形PQNM的面积S=PQNQ=2PQ2,
∵PQ2=PE2+EQ2,
∴S=2(![]() )2=20t2﹣48t+32,
)2=20t2﹣48t+32,
当t=![]() 时,
时,
S最小=20×(![]() )2﹣48×
)2﹣48×![]() +32=
+32=![]() ;
;
②由①点Q坐标为(3﹣2t,0),P(﹣1+t,t),C(3,0),
∴△PQE∽△QNC,可得NC=2QE=8﹣6t,
∴N点坐标为(3,8﹣6t),
由矩形对边平行且相等,P(﹣1+t,t),Q (3﹣2t,0),
∴点M坐标为(3t﹣1,8﹣5t)
当M在抛物线上时,则有
8﹣5t=﹣(3t﹣1)2+3(3t﹣1)+4,
解得t=![]() ,
,
当点Q到A时,Q在抛物线上,此时t=2,
当N在抛物线上时,8﹣6t=4,
∴t=![]() ,
,
综上所述当t=![]() 、
、![]() 或2时,矩形PQNM的顶点落在抛物线上.
或2时,矩形PQNM的顶点落在抛物线上.


科目:初中数学 来源: 题型:
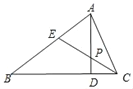
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
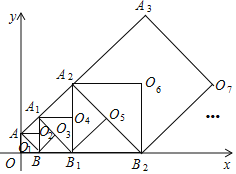
【题目】如图,正方形AOBO2的顶点A的坐标为A(0,2),O1为正方形AOBO2的中心;以正方形AOBO2的对角线AB为边,在AB的右侧作正方形ABO3A1,O2为正方形ABO3A1的中心;再以正方形ABO3A1的对角线A1B为边,在A1B的右侧作正方形A1BB1O4,O3为正方形A1BB1O4的中心;再以正方形A1BB1O4的对角线A1B1为边在A1B1的右侧作正方形A1B1O5A2,O4为正方形A1B1O5A2的中心:…;按照此规律继续下去,则点O2018的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BD⊥AC于点D,∠FAC=![]() ∠ABC,且∠FAC在AC下方.点P,Q分别是射线BD,射线AF上的动点,且点P不与点B重合,点Q不与点A重合,连接CQ,过点P作PE⊥CQ于点E,连接DE.
∠ABC,且∠FAC在AC下方.点P,Q分别是射线BD,射线AF上的动点,且点P不与点B重合,点Q不与点A重合,连接CQ,过点P作PE⊥CQ于点E,连接DE.
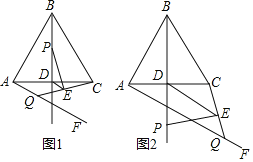
(1)若∠ABC=60°,BP=AQ.
①如图1,当点P在线段BD上运动时,请直接写出线段DE和线段AQ的数量关系和位置关系;
②如图2,当点P运动到线段BD的延长线上时,试判断①中的结论是否成立,并说明理由;
(2)若∠ABC=2α≠60°,请直接写出当线段BP和线段AQ满足什么数量关系时,能使(1)中①的结论仍然成立(用含α的三角函数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
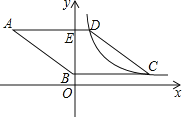
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
某校七年级一班的部分同学和二班的部分同学在元旦期间租小巴车从泸州去成都熊猫繁殖基地看熊猫宝宝,出发地到目的地约![]() ,一班的车速为
,一班的车速为![]() ,二班的车速为
,二班的车速为![]() .
.
(1)生活委员先去超市买大家都喜欢吃的零食“呀!土豆”,但超市的存货不多了,如果每人![]() 包,则剩余
包,则剩余![]() 包:如果每人
包:如果每人![]() 包,则还缺
包,则还缺![]() 包,他们一共有多少人?
包,他们一共有多少人?
(2)因为一班的某同学临时出了些状况,二班的车先走![]() ,一班的车能在到达目的地之前追上二班的车吗?如果能,什么时候追上?
,一班的车能在到达目的地之前追上二班的车吗?如果能,什么时候追上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里:
![]() ,2.525525552…(相邻两个2之间的5的个数逐个加1),0,
,2.525525552…(相邻两个2之间的5的个数逐个加1),0,![]() ,
,![]() ,0.12,
,0.12,![]() ,
,![]() ,
,![]() ,
,![]()
(1)负数集合:{ …};
(2)非负整数集合:{ …};
(3)分数集合:{ …};
(4)无理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BF 是∠ABD 的平分线,CE 是∠ACD 的平分线,BF 与 CE 交于 G,若∠BDC=130°,∠BGC=100°,则∠A 的度数为( )
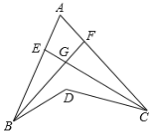
A.60°B.70°C.80°D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com