
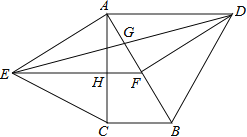
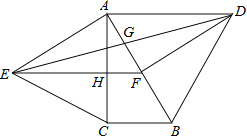
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

【答案】①③④
【解析】试题分析:根据已知先判断△ABC≌△EFA,则∠AEF=∠BAC,得出EF⊥AC,由等边三角形的性质得出∠BDF=30°,从而证得△DBF≌△EFA,则AE=DF,再由FE=AB,得出四边形ADFE为平行四边形而不是菱形,根据平行四边形的性质得出AD=4AG,从而得到答案.
解:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴FE=AB,
∴∠AEF=∠BAC=30°,
∴EF⊥AC,故①正确,
∵EF⊥AC,∠ACB=90°,
∴HF∥BC,
∵F是AB的中点,
∴HF=![]() BC,
BC,
∵BC=![]() AB,AB=BD,
AB,AB=BD,
∴HF=![]() BD,故④说法正确;
BD,故④说法正确;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),
∴AE=DF,
∵FE=AB,
∴四边形ADFE为平行四边形,
∵AE≠EF,
∴四边形ADFE不是菱形;
故②说法不正确;
∴AG=![]() AF,
AF,
∴AG=![]() AB,
AB,
∵AD=AB,
则AD=4AG,故③说法正确,
故答案为:①③④.


科目:初中数学 来源: 题型:
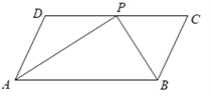
【题目】如图,平行四边形ABCD中,AP,BP分别平分∠DAB和∠CBA,交于DC边上点P,AD=5.
(1)求线段AB的长.
(2)若BP=6,求△ABP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
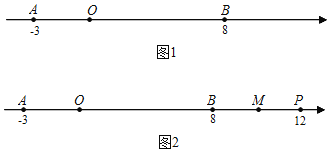
【题目】如果A、B两点在数轴上分别表示有理数a、b,那么它们之间的距离AB=|a﹣b|.如图1,已知数轴上两点A、B对应的数分别为﹣3和8,数轴上另有一个点P对应的数为x
(1)点P、B之间的距离PB= .
(2)若点P在A、B之间,则|x+3|+|x﹣8|= .
(3)①如图2,若点P在点B右侧,且x=12,取BP的中点M,试求2AM﹣AP的值.
②若点P为点B右侧的一个动点,取BP的中点M,那么2AM﹣AP是定值吗?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
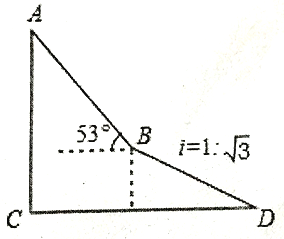
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60![]() 米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l:
米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l: ![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53![]() ,求楼房AC的高度(参考数据:sin53
,求楼房AC的高度(参考数据:sin53![]() =
=![]() , cos53
, cos53![]() =
=![]() , tan53
, tan53![]() =
=![]() ,
, ![]() ≈1.732,结果精确到0.1米)
≈1.732,结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“数形结合”是一种重要的数学思维,观察下面的图形和算式:
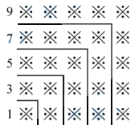
1=1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
解答下列问题:请用上面得到的规律计算:21+23+25+27+…+101=( )
A.2601B.2501C.2400D.2419
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A(-1,3),B(-3,n)两点,直线
的图象交于A(-1,3),B(-3,n)两点,直线![]() 与
与![]() 轴交于点C.
轴交于点C.
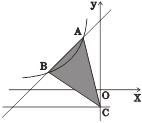
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1 的正方体搭成的立体图形,第(1)个图形由1个正方体搭成,第(2)个图形由4个正方体搭成,第(3)个图形由10个正方体搭成,以此类推,搭成第(6)个图形所需要的正方体个数是( )

A.84个B.56个C.37个D.36个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com