
【题目】如图,平行四边形ABCD中,AP,BP分别平分∠DAB和∠CBA,交于DC边上点P,AD=5.
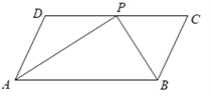
(1)求线段AB的长.
(2)若BP=6,求△ABP的周长.
【答案】(1)10cm;(2)24cm.
【解析】
(1)根据角平分线定义和平行线性质得∠DAP=∠BAP,∠DPA=∠PAB,等量代换得∠DAP=∠DPA,由等腰三角形性质可得DA=DP ;同理可得 CB=CP,由DC=DP+CP即可求得答案.
(2)据角平分线定义得∠BAP=![]() ∠BAD,∠PBA=
∠BAD,∠PBA=![]() ∠CBA, 由平行线性质得∠DAB+∠ABC=180°,从而可得 ∠PAB+∠PBA=90°,在Rt△APB中,根据勾股定理求得AP长,再由三角形周长即可求得答案.
∠CBA, 由平行线性质得∠DAB+∠ABC=180°,从而可得 ∠PAB+∠PBA=90°,在Rt△APB中,根据勾股定理求得AP长,再由三角形周长即可求得答案.
解:(1)在平行四边形ABCD中,
∵AP平分∠DAB,
∴∠DAP=∠BAP,
∵DC//AB,
∴∠DPA=∠PAB,
∴∠DAP=∠DPA,
∴DA=DP.
同理CB=CP,
∴AD=BC=5,
∴DC=DP+CP=10cm.
(2)∵DA//CP,
∴∠DAB+∠ABC=180° ,
∵AP平分∠DAB,BP平分∠ABC
∴∠BAP= ![]() ∠BAD,∠PBA=
∠BAD,∠PBA= ![]() ∠CBA,
∠CBA,
∴∠PAB+∠PBA=90,
∴∠APB=90,
∵AB=10,BP=6,
∴PA=8,
∴C△ABP=24cm.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:
【题目】李明同学早上骑自行车上学,中途因道路施工需步行一段路,到学校共用时18分钟,他骑自行车的平均速度是300米/分钟,步行的平均速度是120米/分钟,他家离学校的距离是4500米.
(1)李明上学时骑自行车的路程和步行的路程分别为多少米?
(2)放学后李明从17:40开始离校回家,但此时道路施工的地段增长了600米,如果按照上学时的速度,问李明能否在18:00之前到家?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,抛物线y=ax2+bx+3与x轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.
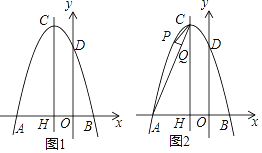
(1)求抛物线的表达式;
(2)点E,F分别是抛物线对称轴CH上的两个动点(点E在点F上方),且EF=1,求使四边形BDEF的周长最小时的点E,F坐标及最小值;
(3)如图2,点P为对称轴左侧,x轴上方的抛物线上的点,PQ⊥AC于点Q,是否存在这样的点P使△PCQ与△ACH相似?若存在请求出点P的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
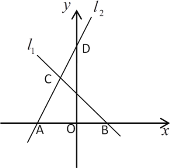
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() (0,5),与直线
(0,5),与直线![]() 交于点
交于点![]() (﹣1,
(﹣1,![]() ),且与
),且与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
(2)求△![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E,构造出平行四边形AEDF.
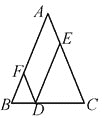
(1)若点D在线段BC上时. ①求证:FB=FD.②求证:DE+DF=AC.
(2)点D在边BC所在的直线上,若AC=8,DE=3,请作出简单示意图求DF的长度,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:

(1)已知x3+27有一个因式x+3,用待定系数法分解:x3+27.
(2)观察上述因式分解,直接写出答案:因式分解:a3+b3=_______;a3-b3=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com