
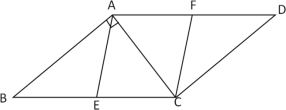
【题目】如图,已知点![]() ,
,![]() 分别是平行四边形
分别是平行四边形![]() 的边
的边![]() ,
,![]() 上的中点,且∠
上的中点,且∠![]() =90°.
=90°.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() =4,
=4,![]() =5,求菱形
=5,求菱形![]() 的面积.
的面积.
【答案】(1)见解析;(2)10.
【解析】
(1)由平行四边形的性质可得BC=AD,BC∥AD,由中点的性质可得EC=AF,可证四边形AECF为平行四边形,由直角三角形的性质可得AE=EC,即可得结论;
(2)可求S△ABC=![]() AB×AC=10,即可求菱形AECF的面积.
AB×AC=10,即可求菱形AECF的面积.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的中点
上的中点
∴AF∥EC ,AF=EC
∴四边形AECF是平行四边形.
在Rt△ABC中,∠BAC=90°,点E是BC边的中点,
∴AE =![]() BC=CE
BC=CE
∴平行四边形AECF是菱形.
(2)∵∠BAC=90°,AB=5,AC=4,
∴S△ABC=![]() AB×AC=10
AB×AC=10
∵点E是BC的中点,
∴S△AEC=![]() S△ABC=5
S△ABC=5
∵四边形AECF是菱形
∴四边形AECF的面积=2S△AEC=10.


科目:初中数学 来源: 题型:
【题目】淮安日报社为了了解市民“获取新闻的主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.

请根据图表信息解答下列问题:
(1)统计表中的m= ,n= ;
(2)并请补全条形统计图;
(3)若该市约有80万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一边长为36cm的正方形硬纸板进行适当的剪裁,折成一个长方体盒子(纸板的厚度忽略不计)
(1)如图,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方体盒子.
①要使折成的长方体盒子的底面积为676cm2,那么剪掉的正方形的边长为多少?
②折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方体盒子,若折成的一个长方体盒子的表面积为880cm2,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AP,BP分别平分∠DAB和∠CBA,交于DC边上点P,AD=5.
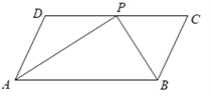
(1)求线段AB的长.
(2)若BP=6,求△ABP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有两个小机器人A、B在一条笔直的道路上由西向东行走,两机器人相距6cm,即AB=6cm.其中机器人A的速度为3cm/s,机器人B的速度为2cm/s.设机器人B行走的时间为t(s).
(1)若两机器人同时出发,
①当t=![]() 时,AB= cm;当t=7时,AB= cm;
时,AB= cm;当t=7时,AB= cm;
②当两机器人相距4cm时,求机器人B行走的时间t的值;
(2)若机器人B先行走2s,机器人A再行走,当两机器人相距10cm时,请直接写出t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF,
(1)求证:AE=CF;
(2)若AB=3,∠AOD=120°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
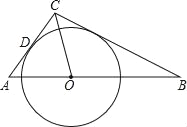
【题目】如图,在△ABC中,∠C=90°,∠ACB的平分线交AB于点O,以O为圆心的⊙O与AC相切于点D.
(1)求证:⊙O与BC相切;
(2)当AC=3,BC=6时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
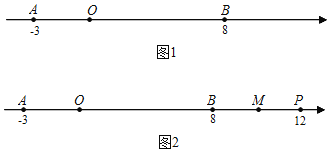
【题目】如果A、B两点在数轴上分别表示有理数a、b,那么它们之间的距离AB=|a﹣b|.如图1,已知数轴上两点A、B对应的数分别为﹣3和8,数轴上另有一个点P对应的数为x
(1)点P、B之间的距离PB= .
(2)若点P在A、B之间,则|x+3|+|x﹣8|= .
(3)①如图2,若点P在点B右侧,且x=12,取BP的中点M,试求2AM﹣AP的值.
②若点P为点B右侧的一个动点,取BP的中点M,那么2AM﹣AP是定值吗?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com