
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
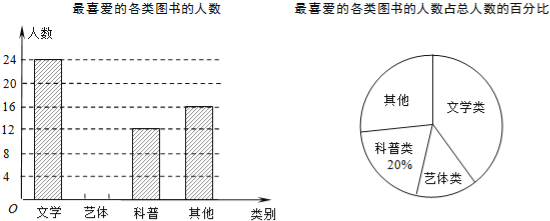
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1,当点A1落在AC上时.
(1)如图,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
(2)如图,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
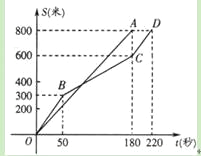
A、小莹的速度随时间的增大而增大B、小梅的平均速度比小莹的平均速度大
C、在起跑后180秒时,两人相遇D、在起跑后50秒时,小梅在小莹的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)

(1)本次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AC是对角线,点E,F,G分别为AB,AC,BC的中点:
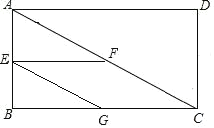
(1)求证:四边形EFCG是平行四边形;
(2)若ACD2ACB,AB4,求BF的长;
(3)在(2)的条件下,求四边形EFCG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学从家到学校的距离之比是10:7,甲同学的家与学校的距离为3000米,甲同学乘公交车去学校、乙同学骑自行车去学校.已知公交车速度是乙骑自行车速度的2倍,甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙同学的家与学校的距离为多少米?
(2)求乙骑自行车的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com