
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E,构造出平行四边形AEDF.
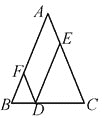
(1)若点D在线段BC上时. ①求证:FB=FD.②求证:DE+DF=AC.
(2)点D在边BC所在的直线上,若AC=8,DE=3,请作出简单示意图求DF的长度,不需要证明.
【答案】(1)见解析,见解析;(2)DF=BF=5或DF=BF=11 见解析.
【解析】
(1)①根据等腰三角形性质得∠B=∠C,由平行线性质得∠FDB=∠C,等量代换得∠B=∠FDB,根据等腰三角形性质:等角对等边即可得证.
②由平行四边形性质得ED=AF,AE=FD,由①知FB=FD,等量代换得AE=FB,从而可得DE+DF= AF+ FB=AB=AC.
(2)如图1:根据平行四边形性质得AF=DE=3,DF=AE,由(1)知FB=FD,由DF=BF=AB-AF=8-3=5;
如图2:根据平行四边形性质得AF=DE=3,DF=AE,由(1)知FB=FD,由DF=BF=AB+AF=8+3=11.
解:(1)①∵AB=AC,
∴∠B=∠C,
∵DF//AC,
∴∠FDB=∠C,
∴∠B=∠FDB,
∴FB=FD.
②∵四边形AEDF是平行四边形,
∴ED=AF,AE=FD,
∵FB=FD,
∴AE=FB,
∴DE+DF= AF+ FB=AB,
∵AB=AC,
∴DE+DF=AC.
(2)如图1,

∵四边形AEDF为平行四边形,
∴AF=DE,DF=AE,
由(1)知FB=FD,
∵AC=8,DE=3,AB=AC,
∴AF=3,BF=AB-AF=8-3=5,
∴DF=BF=5;
如图2,

∵四边形AEDF为平行四边形,
∴AF=DE,DF=AE,
由(1)知FB=FD,
∵AC=8,DE=3,AB=AC,
∴AF=3,BF=AB+AF=8+3=11,
∴DF=BF=11;


科目:初中数学 来源: 题型:
【题目】已知:一次函数y=﹣x+b的图象与x轴、y轴的交点分别为A、B与反比例函数![]() 的图象交于点C、D,且
的图象交于点C、D,且![]() .
.
(1)求∠BAO的度数;
(2)求O到DC的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
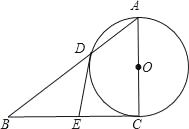
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.
(1)求证:DE=![]() BC;
BC;
(2)若四边形ODEC是正方形,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7张如图1的长为![]() ,宽为b
,宽为b![]() 的小长方形纸片,按如图2、3的方式不重叠地放在 矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.
的小长方形纸片,按如图2、3的方式不重叠地放在 矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.
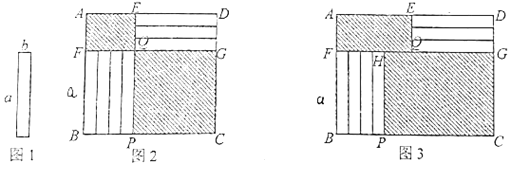
(1)如图2,点E、Q、P在同一直线上,点F、Q、G在同一直线上,右下角与左上角的阴影部分的面积的差为____________(用含![]() 、
、![]() 的代数式表示),矩形ABCD的面积为____________(用含
的代数式表示),矩形ABCD的面积为____________(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)如图3,点F、H、Q、G在同一直线上,设右下角与左上角的阴影部分的面积的差为S,![]() .
.
①用![]() 、
、![]() 、
、![]() 的代数式表示AE;
的代数式表示AE;
②当BC的长度变化时,按照同样的放置方式,S始终保持不变,那么![]() 、
、![]() 必须满足什么条件?
必须满足什么条件?
查看答案和解析>>
科目:初中数学 来源: 题型:
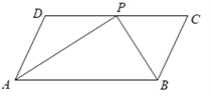
【题目】如图,平行四边形ABCD中,AP,BP分别平分∠DAB和∠CBA,交于DC边上点P,AD=5.
(1)求线段AB的长.
(2)若BP=6,求△ABP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF,
(1)求证:AE=CF;
(2)若AB=3,∠AOD=120°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警车在一条南北大道上巡逻,某天巡警车从岗亭![]() 处出发,规定向北方向为正,当天行驶纪录如下(单位:千米)
处出发,规定向北方向为正,当天行驶纪录如下(单位:千米)
﹣10,﹣9,+7,﹣15,+6,﹣5,+4,﹣2
![]()
(1)最终巡警车是否回到岗亭![]() 处?若没有,在岗亭何方,距岗亭多远?
处?若没有,在岗亭何方,距岗亭多远?
(2)摩托车行驶1千米耗油0.2升,油箱有油10升,够不够?若不够,途中还需补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A(-1,3),B(-3,n)两点,直线
的图象交于A(-1,3),B(-3,n)两点,直线![]() 与
与![]() 轴交于点C.
轴交于点C.
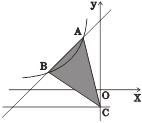
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com