
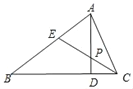
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.
【答案】(1)证明见解析;(2)30°.
【解析】
由三角形的内角和可求出∠ECB=35°,根据角平分线的定义可求∠ACB=70°,进而可求出∠BAC=70°,从而结论可证;
(2)由AP是△AEC边EC上的中线可知AP=PC,从而∠PAC=∠PCA,由CE是∠ACB的平分线,可证∠PAC=∠PCA=∠PCD,从而可求出∠PAC的度数,然后求出∠BAD=60°,继而可求出∠B的值.
(1)证明:∵∠B=40°,∠AEC=75°,
∴∠ECB=∠AEC﹣∠B=35°,
∵CE平分∠ACB,
∴∠ACB=2∠BCE=70°,
∠BAC=180°﹣∠B﹣∠ACB=180°﹣40°﹣70°=70°,
∴∠BAC=∠BCA,
∴AB=AC.
(2)∵∠BAC=90°,AP是△AEC边EC上的中线,
∴AP=PC,
∴∠PAC=∠PCA,
∵CE是∠ACB的平分线,
∴∠PAC=∠PCA=∠PCD,
∵∠ADC=90°,
∴∠PAC=∠PCA=∠PCD=90°÷3=30°,
∴∠BAD=60°,
∵∠ADB=90°,
∴∠B=90°﹣60°=30°.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ABE绕点![]() 顺时针旋转90
顺时针旋转90![]() 后,得到△ACF,连接DF.下列结论中:①∠DAF=45° ②△
后,得到△ACF,连接DF.下列结论中:①∠DAF=45° ②△![]() ≌△
≌△![]() ③AD平分∠EDF ④
③AD平分∠EDF ④![]() ;正确的有______________(填序号)
;正确的有______________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(﹣1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )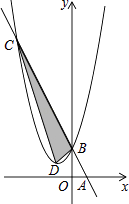
A.8:1
B.6:1
C.5:1
D.4:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1: ![]() ,求旗杆AB的高度(
,求旗杆AB的高度( ![]() ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图a是长方形纸带(提示:AD∥BC),将纸带沿EF折叠成图b,再沿GF折叠成图c.

(1)若∠DEF=20°,则图b中∠EGB=______,∠CFG=______;
(2)若∠DEF=20°,则图c中∠EFC=______;
(3)若∠DEF=α,把图c中∠EFC用α表示为______;
(4)若继续按EF折叠成图d,按此操作,最后一次折叠后恰好完全盖住∠EFG,整个过程共折叠了9次,问图a中∠DEF的度数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求一次函数的解析式;
(2)判断点C(4,-2)是否在该一次函数的图象上,说明理由;
(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
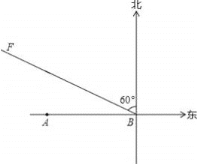
【题目】如图,A市气象站测得台风中心在A市正东方向300千米的B处,以10![]() 千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
(1)A市是否会受到台风的影响?写出你的结论并给予说明;
(2)如果A市受这次台风影响,那么受台风影响的时间有多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com