
【题目】如图,A市气象站测得台风中心在A市正东方向300千米的B处,以10![]() 千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
(1)A市是否会受到台风的影响?写出你的结论并给予说明;
(2)如果A市受这次台风影响,那么受台风影响的时间有多长?
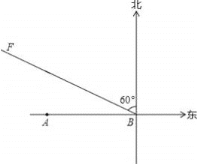
【答案】过点A作AC⊥BF于C,
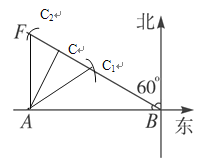
则AC=150千米,![]() ,故A市会受到台风的影响,
,故A市会受到台风的影响,
以A为圆心,200km为半径作弧交BF于C1、C2两点,连接AC1=AC2
∵AC⊥BF,
∴C1C2=2C1C.
在Rt△ACC1中,有C1C=![]() ,
,
∴C1C2=![]() km,
km,
∴A城受台风干扰的时间为:![]() (小时).
(小时).
【解析】
(1)会.理由如下:如图所示,过点A作AD⊥BF于D,
在Rt△ABD中,∠ABD=30°,AB=300千米.
∴![]() (千米).
(千米).
又∵AD=150千米<200千米,
∴A市会受台风影响.
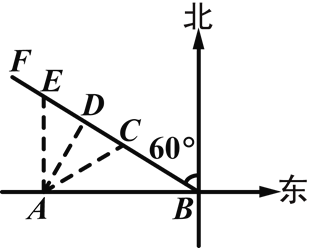
(2)设C点刚好受台风影响,E点刚好不受台风影响,则AC=AE=200千米.
在Rt△ADC中,由勾股定理得
![]() (千米),
(千米),
∴![]() 千米.
千米.
∴A市受台风影响的时间为![]() (小时).
(小时).


科目:初中数学 来源: 题型:
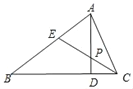
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地保护环境,某市污水处理厂决定先购买A,B两型污水处理设备共20台,对周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知2台A型污水处理设备和1台B型污水处理设备每周可以处理污水680吨,4台A型污水处理设备和3台B型污水处理设备每周可以处理污水1560吨.
(1)求A、B两型污水处理设备每周每台分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案.
(3)如果你是厂长,从节约资金的角度来谈谈你会选择哪种方案并说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1,第2次平移长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2,…,第n次平移长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),若ABn的长度为2 026,则n的值为( ).
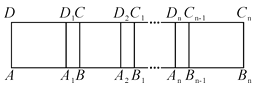
A. 407B. 406C. 405D. 404
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有个点![]() ,点
,点![]() 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点![]() ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点![]() ,第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第200次跳动至点
,第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第200次跳动至点![]() 的坐标是( )
的坐标是( )

A. (51,100)B. (50,100)C. (-50,100)D. (-51,100)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,M是边AB的中点,CH⊥AB于点H,CD平分∠ACB.

(1)求证:∠1=∠2.
(2)过点M作AB的垂线交CD的延长线于点E,连结AE,BE.求证:CM=EM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数。
解:∵EF∥AD,
∴∠2= ( )
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°,∴∠AGD= 。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com