
【题目】如图,在Rt△ABC中,∠ACB=90°,M是边AB的中点,CH⊥AB于点H,CD平分∠ACB.

(1)求证:∠1=∠2.
(2)过点M作AB的垂线交CD的延长线于点E,连结AE,BE.求证:CM=EM.
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:
(1)由CD平分∠ACB可得∠ACD=∠BCD,我们只需证∠ACM=∠BCH就可得∠1=∠2;而由CM是Rt△ABC斜边上的中线易得AM=CM,由此可得∠ACM=∠A,而由已知易证∠A=∠BCH,从而可得∠ACM=∠BCH;
(2)由CH⊥AB,ME⊥AB可得ME∥CH,由此可得∠E=∠1=∠2,就可得CM=ME.
试题解析:
(1)∵∠ACB=90°,
∴∠A+∠B=90°.
∵CH⊥AB,
∴∠B+∠BCH=90°,
∴∠A=∠BCH.
∵M是斜边AB的中点,
∴CM=AM,
∴∠A=∠ACM.
∴∠BCH=∠ACM.
∵CD平分∠ACB,
∴∠BCD=∠ACD,
∴∠BCD-∠BCH=∠ACD-∠ACM,
即∠1=∠2.
(2)∵CH⊥AB,ME⊥AB,
∴ME∥CH,
∴∠1=∠E.
∵∠1=∠2,
∴∠2=∠MED,
∴CM=EM.


科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE, OP⊥CD,∠ABO=40°,则下列结论:①∠BO E=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有(填序号)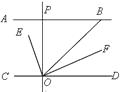
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正六边形ABCDEF在直角坐标系内的位置如图所示,点A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转.若每次翻转60°,则经过2017次翻转之后,点B的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
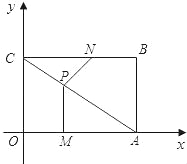
【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.
(1)P点的坐标为多少(用含x的代数式表示);
(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;
(3)当x为何值时,△NPC是一个等腰三角形?简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则一次性购买盒子所需要最少费用为 元.
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com