
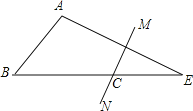
【题目】如图所示,在![]() 中,
中,![]() ,AE的垂直平分线MN交BE于点C,且
,AE的垂直平分线MN交BE于点C,且![]() ,则
,则![]() 的度数是______.
的度数是______.
【答案】![]()
【解析】
首先连接AC,由AE的垂直平分线MN交BE于点C,可得AC=EC,又由AB+BC=BE,易证得AB=AC,然后由等腰三角形的性质与三角形内角和定理,求得∠BAE=∠BAC+∠CAE=180°-4∠E+∠E=105°,继而求得答案.
连接AC,
∵MN是AE的垂直平分线,
∴AC=EC,
∴∠CAE=∠E,
∵AB+BC=BE,BC+EC=BE,
∴AB=EC=AC,
∴∠B=∠ACB,
∵∠ACB=∠CAE+∠E=2∠E,
∴∠B=2∠E,
∴∠BAC=180°-∠B-∠ACB=180°-4∠E,
∵∠BAE=∠BAC+∠CAE=180°-4∠E+∠E=105°,
解得:∠E=25°,
∴∠B=2∠E=50°.
故答案为:50°.


科目:初中数学 来源: 题型:
【题目】如图a是长方形纸带(提示:AD∥BC),将纸带沿EF折叠成图b,再沿GF折叠成图c.

(1)若∠DEF=20°,则图b中∠EGB=______,∠CFG=______;
(2)若∠DEF=20°,则图c中∠EFC=______;
(3)若∠DEF=α,把图c中∠EFC用α表示为______;
(4)若继续按EF折叠成图d,按此操作,最后一次折叠后恰好完全盖住∠EFG,整个过程共折叠了9次,问图a中∠DEF的度数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c为△ABC的三条边的长,且满足b2+2ab=c2+2ac.
(1)试判断△ABC的形状,并说明理由;
(2)若a=6,b=5,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
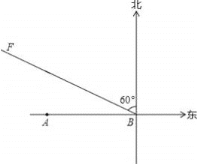
【题目】如图,A市气象站测得台风中心在A市正东方向300千米的B处,以10![]() 千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
(1)A市是否会受到台风的影响?写出你的结论并给予说明;
(2)如果A市受这次台风影响,那么受台风影响的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1 , 连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2 , 连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3 , …,如此继续,可以依次得到点O4 , O5 , …,On和点E4 , E5 , …,En . 则OnEn=AC.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,AB=2![]() ,∠A=120°,点P、Q、K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
,∠A=120°,点P、Q、K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
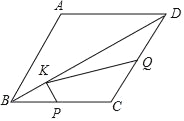
A. 1 B. 3 C. ![]() D.
D. ![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.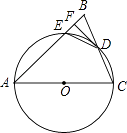
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com