
【题目】如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1 , 连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2 , 连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3 , …,如此继续,可以依次得到点O4 , O5 , …,On和点E4 , E5 , …,En . 则OnEn=AC.(用含n的代数式表示)
科目:初中数学 来源: 题型:
【题目】如图,已知直角坐标系中,A、B、D三点的坐标分别为A(8,0),B(0,4),D(﹣1,0),点C与点B关于x轴对称,连接AB、AC.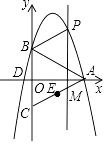
(1)求过A、B、D三点的抛物线的解析式;
(2)有一动点E从原点O出发,以每秒2个单位的速度向右运动,过点E作x轴的垂线,交抛物线于点P,交线段CA于点M,连接PA、PB,设点E运动的时间为t(0<t<4)秒,求四边形PBCA的面积S与t的函数关系式,并求出四边形PBCA的最大面积;
(3)抛物线的对称轴上是否存在一点H,使得△ABH是直角三角形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
步骤1:分别以点A,D为圆心,以大于 ![]() AD的长为半径,在AD两侧作弧,两弧交于点M,N;
AD的长为半径,在AD两侧作弧,两弧交于点M,N;
步骤2:连接MN,分别交AB,AC于点E,F;
步骤3:连接DE,DF.
下列叙述不一定成立的是( )
A.线段DE是△ABC的中位线
B.四边形AFDE是菱形
C.MN垂直平分线段AD
D.![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③甲队比乙队提前3天完成任务;
④当x=2或6时,甲乙两队所挖管道长度都相差100米.
正确的有 . (在横线上填写正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有个点![]() ,点
,点![]() 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点![]() ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点![]() ,第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第200次跳动至点
,第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第200次跳动至点![]() 的坐标是( )
的坐标是( )

A. (51,100)B. (50,100)C. (-50,100)D. (-51,100)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,并在∠MON内部作射线OC.
(1)如图1,三角板的一边ON与射线OB重合,且∠AOC=150°.若以点O为观察中心,射线OM表示正北方向,求射线OC表示的方向;
(2)如图2,将三角板放置到如图位置,使OC恰好平分∠MOB,且∠BON=2∠NOC,求∠AOM的度数;
(3)若仍将三角板按照如图2的方式放置,仅满足OC平分∠MOB,试猜想∠AOM与∠NOC之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).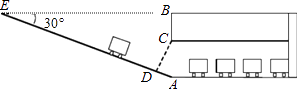
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com