
����Ŀ����֪��OΪֱ��AB��һ�㣬��ֱ�����ǰ�MON��ֱ�Ƕ�����ڵ�O�������ڡ�MON�ڲ�������OC��
��1����ͼ1�����ǰ��һ��ON������OB�غϣ��ҡ�AOC��150�������Ե�OΪ�۲����ģ�����OM��ʾ��������������OC��ʾ�ķ���
��2����ͼ2�������ǰ���õ���ͼλ�ã�ʹOCǡ��ƽ�֡�MOB���ҡ�BON��2��NOC�����AOM�Ķ�����
��3�����Խ����ǰ尴����ͼ2�ķ�ʽ���ã�������OCƽ�֡�MOB���Բ����AOM���NOC֮���������ϵ����˵�����ɣ�

���𰸡���1������OC��ʾ�ķ���Ϊ��ƫ��60������2��45������3����AOM��2��NOC.
��������
��1�����ݡ�MOC����AOC����AOM�������ݼ��㣬���ó�����OC��ʾ�ķ���
��2�����ݽǵı��ֹ�ϵ�Լ���ƽ���ߵĶ��弴����⣻
��3�����NOCΪ������AOMΪ������MOC��90�����������ݡ�AOM+��MOC+��BOC��180�����ɵõ���AOM���NOC�����������ϵ��
��1���ߡ�MOC����AOC����AOM��150����90����60����
������OC��ʾ�ķ���Ϊ��ƫ��60����
��2���ߡ�BON��2��NOC��OCƽ�֡�MOB��
���MOC����BOC��3��NOC��
�ߡ�MOC+��NOC����MON��90����
��3��NOC+��NOC��90����
��4��NOC��90����
���BON��2��NOC��45����
���AOM��180������MON����BON��180����90����45����45����
��3����AOM��2��NOC��
���NOC������AOM������MOC��90��������
�ߡ�AOM+��MOC+��BOC��180����
����+90������+90��������180����
������2����0��������2����
���AOM��2��NOC��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У����ڼ�������ǣ� ��
A.��һ�������ȵ�����ֱ��������һ������
B.�Խ�����ȵ�������������
C.������Y=X2��20x+17�Ŀ�������
D.��һ������ͼ���������У������⳯�ϵ�Ƶ��Ϊ3��5���⳯�ϵĸ���ҲΪ3��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��cΪ��ABC�������ߵij���������b2+2ab=c2+2ac.
(1)���жϡ�ABC����״����˵�����ɣ�
(2)��a=6��b=5�����ABC�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪CO1�ǡ�ABC�����ߣ�����O1��O1E1��AC��BC�ڵ�E1 �� ����AE1��CO1�ڵ�O2������O2��O2E2��AC��BC�ڵ�E2 �� ����AE2��CO1�ڵ�O3������O3��O3E3��AC��BC�ڵ�E3 �� ������˼������������εõ���O4 �� O5 �� ����On�͵�E4 �� E5 �� ����En �� ��OnEn=AC�����ú�n�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪a+b����![]() �������ʽ��a��1��2+b��2a+b��+2a��ֵ��
�������ʽ��a��1��2+b��2a+b��+2a��ֵ��
��2����֪a��b��c�������ε����ߣ���a2+b2+c2��ab��bc��ac��0����֤�����������ǵȱ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�У�AB��2![]() ����A��120������P��Q��K�ֱ�Ϊ�߶�BC��CD��BD�ϵ�����һ�㣬��PK+QK����СֵΪ��������
����A��120������P��Q��K�ֱ�Ϊ�߶�BC��CD��BD�ϵ�����һ�㣬��PK+QK����СֵΪ��������
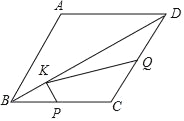
A. 1 B. 3 C. ![]() D.
D. ![]() +1
+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
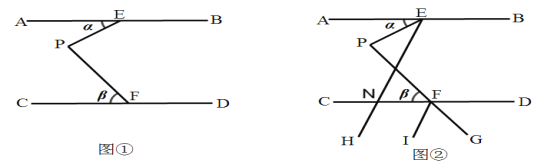
����Ŀ����ͼ�٣���֪AB��CD����E��F�ֱ���AB��CD�ϵĵ㣬��P����ƽ����֮���һ�㣬���AEP=������PFC=������ͼ���У�����E������EH��CD�ڵ�N��������FI���ӳ�PF��G��ʹ��PE��FG�ֱ�ƽ�֡�AEH����DFI���õ�ͼ�ڣ�
��1����ͼ���У�����=20������=50��ʱ�����EPF�Ķ�����
��2���ڣ�1���������£���ͼ���С�END���CFI�Ķ�����
��3����ͼ���У���FI��EHʱ���������������������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽���о�����֪����ABC�͡�CDE���ǵȱ������Σ�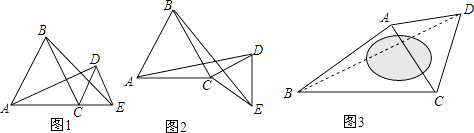
��1����ͼ1������A��C��E��һ��ֱ����ʱ�����ǿ��Եõ����ۣ��߶�AD��BE��������ϵΪ�� ��
�߶�AD��BE���ɵ���Ƕ���Ϊ�㣻
��2����ͼ2������A��C��E����һ��ֱ����ʱ����֤����1���еĽ�����Ȼ������
������ã�
��ͼ3��ij�㳡��һ���ı�������ABCD���ֲ�ã�AB=60m��BC=80m���ҡ�ABC=30�㣬��DAC=��DCA=60�㣬����ˮ������B��D����֮��ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ��DΪBC��һ�㣬��AB=AC=BD����ͼ�С�1���2�Ĺ�ϵ�ǣ� ��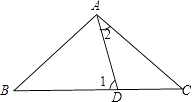
A.��1=2��2
B.��1+��2=180��
C.��1+3��2=180��
D.3��1����2=180��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com