
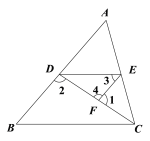
【题目】探索研究:已知:△ABC和△CDE都是等边三角形.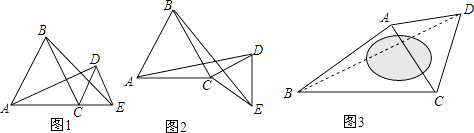
(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为: ,
线段AD与BE所成的锐角度数为°;
(2)如图2,当点A、C、E不在一条直线上时,请证明(1)中的结论仍然成立;
灵活运用:
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离.
【答案】
(1)相等,60
(2)解:如图3,以AB为边在△ABC外侧作等边△ABE,连接CE.
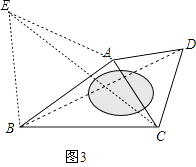
由(2)可得:BD=CE
∴∠EBC=60°+30°=90°,
∴△EBC是直角三角形
∵EB=60m BC=80m,
∴CE= ![]() =
= ![]() =100(m).
=100(m).
∴水池两旁B、D两点之间的距离为100m.
【解析】解:(1)如图1,
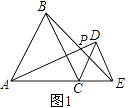
∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC,
由三角形的外角性质,∠DPE=∠PEA+∠DAC,
∠DCE=∠ADC+∠DAC,
∴∠DPE=∠DCE=60°;
所以答案是:相等,60;
⑵如图2,

∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠DAC=∠EBC,
∴∠BPA=180°﹣∠ABP﹣∠BAP=180°﹣∠ABC﹣∠BAC=60°.
【考点精析】通过灵活运用等边三角形的性质,掌握等边三角形的三个角都相等并且每个角都是60°即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
步骤1:分别以点A,D为圆心,以大于 ![]() AD的长为半径,在AD两侧作弧,两弧交于点M,N;
AD的长为半径,在AD两侧作弧,两弧交于点M,N;
步骤2:连接MN,分别交AB,AC于点E,F;
步骤3:连接DE,DF.
下列叙述不一定成立的是( )
A.线段DE是△ABC的中位线
B.四边形AFDE是菱形
C.MN垂直平分线段AD
D.![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,并在∠MON内部作射线OC.
(1)如图1,三角板的一边ON与射线OB重合,且∠AOC=150°.若以点O为观察中心,射线OM表示正北方向,求射线OC表示的方向;
(2)如图2,将三角板放置到如图位置,使OC恰好平分∠MOB,且∠BON=2∠NOC,求∠AOM的度数;
(3)若仍将三角板按照如图2的方式放置,仅满足OC平分∠MOB,试猜想∠AOM与∠NOC之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).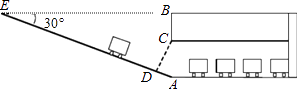
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知∠1+∠2=180°,∠3=∠B 求证:∠AED=∠ACB
证明:∵∠1+∠4=180°(平角定义)
∠1+∠2=180°(已知)
∴_____________( )
∴ ∥ ( )
∴∠3+∠ =180°( )
又∵∠3=∠B(已知)
∴∠ +∠ =180°(等量代换)
∴ ∥ ( )
∴∠AED=∠ACB( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某营业厅对手机话费业务有如下的优惠:
优惠规则:
①用户手机账户原有话费不能低于240元;
②办理业务时,首先从手机账户中一次性扣除240元,并把这240元抵为300元话费,然后将这300元话费分12次,在每月的15号等额返还到手机账户;
③每月1号从手机账户中扣除话费49元,当月不再扣除其他任何费用;
④每月1号手机账户的话费余额不足以扣除49元时,视为欠费,则当月不再返还等额的话费.
小明的手机账户中原有话费400元,办理了这项优惠业务,设小明的手机账户中每个月末的话费余额是y(元),月数为x(个),则
(1)每个月等额返还的话费是元,第2个月末的话费余额是元;
(2)求y关于x的函数关系式;
(3)若不续费,小明的手机第几个月会欠费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,过等腰直角三角形ABC的直角顶点A作直线AP,点B关于直线AP的对称点为E,连接BE,CE,其中CE交直线AP于点F.
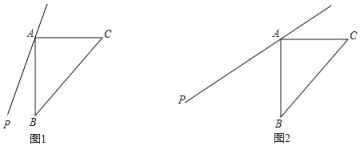
(1)依题意补全图形;
(2)若∠PAB=16°,求∠ACF的度数;
(3)如图2,若45°<∠PAB<90°,用等式表示线段AB,FE,FC之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x<100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x<100 | b | 0.06 |
合计 | 1 |

根据以上信息解答下列问题:
(1)统计表中c的值为________;样本成绩的中位数落在分数段________中;
(2)补全频数直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评的作品数量是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com