
【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x<100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x<100 | b | 0.06 |
合计 | 1 |

根据以上信息解答下列问题:
(1)统计表中c的值为________;样本成绩的中位数落在分数段________中;
(2)补全频数直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评的作品数量是多少.
【答案】(1)0.34;70≤x<80;(2)见解析;(3) 180幅.
【解析】
(1)由60≤x<70频数和频率求得总数,根据频率=频数÷总数求得a、b、c的值,由中位数定义求解可得;
(2)根据(1)中所求数据补全图形即可得;
(3)总数乘以80分以上的频率即可.
解:(1)本次调查的作品总数为18÷0.36=50(幅),
则c=17÷50=0.34,a=50×0.24=12,b=50×0.06=3,
其中位数为第25、26个数的平均数,
∴中位数落在70≤x<80中,
故答案为:0.34,70≤x<80;
(2)补全图形如下:
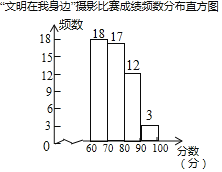
(3)600×(0.24+0.06)=180(幅),
答:估计全校被展评作品数量是180幅.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】探索研究:已知:△ABC和△CDE都是等边三角形.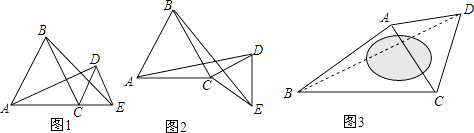
(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为: ,
线段AD与BE所成的锐角度数为°;
(2)如图2,当点A、C、E不在一条直线上时,请证明(1)中的结论仍然成立;
灵活运用:
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图所示,D为BC上一点,且AB=AC=BD,则图中∠1与∠2的关系是( )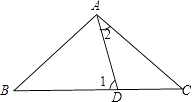
A.∠1=2∠2
B.∠1+∠2=180°
C.∠1+3∠2=180°
D.3∠1﹣∠2=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a、b,定义运算:“★”,当a≥b时,a★b=2a-3b,当a<b时,a★b=![]() .
.
(1)计算:(x+2)★(x+1)的值;
(2)若(x+1)★(2x-1)=-1,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线y= ![]() 与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= ![]() .
.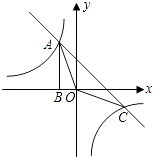
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
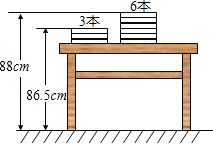
【题目】如图,两摞规格完全相同的课本整齐叠放在讲台上请根据图中所给出的数据信息,回答下列问题:
(1)每本课本的厚度为______cm;
(2)若有一摞上述规格的课本x本,整齐叠放在讲台上,请用含x的代数式表示出这一摞数学课本的顶部距离地面的高度为______cm;
(3)当x=48时,若从中取走10本,求余下的课本的顶部距离地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着出行方式的多样化,某地区打车有三种乘车方式,收费标准如下(假设打车的平均车速为30千米/小时):
网约出租车 | 网约顺风车 | 网约专车 |
3千米以内:12元 | 1.5元/千米 | 2元/千米 |
超过3千米的部分:2.4元/千米 | 0.5元/分钟 | 0.6元/分钟 |
(如:乘坐6千米,耗时12分钟,网约出租车的收费为:12+2.4×(6-3)=19.2(元);网约顺风车的收费为:6×1.5+12×0.5=15(元);网约专车的收费为:6×2+12×0.6=19.2(元))
请据此信息解决如下问题:
(1)王老师乘车从纵棹园去汽车站,全程8千米,如果王老师乘坐网约出租车,需要支付的打车费用为______元;
(2)李校长乘车从纵掉园去生态园,乘坐网约顺风车比乘坐网约出租车节省了2元.求从纵棹园去生态园的路程;
(3)网约专车为了和网约顺风车竞争客户,分别推出了优惠方式:网约顺风车对于乘车路程在5千米以上(含5千米)的客户每次收费立减6元;网约专车打车车费一律七五折优惠.对采用哪一种打车方式更合算提出你的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小华利用含30°角的三角板测量楼房高度的示意图,已知桌子高AB为1米,地面上B和D之间的距离为100米,则楼高CD约为( ) 
A.51米
B.59米
C.88米
D.174米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com